Прямоугольная декартовая система координат

Прямоугольная декартовая система координат - это способ получения ортогональных проекций, обладающих обратимостью.

Положение точки (а следовательно, и любой геометрической фигуры) в пространстве может быть определено, если будет задана какая-либо координатная системе отнесения. Наиболее удобной для фиксирования положения геометрической фигуры в пространстве и выявления ее формы по ортогональным проекциям является прямоугольная декартовая система координат, состоящая из трех взаимно перпендикулярных плоскостей.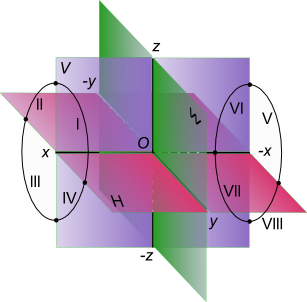

Прямоугольная декартовая система координат

Рассмотрим макет из трех взаимно перпендикулярных плоскостей изображенный на рисунке.

Условимся называть:
- плоскость H - горизонтальной плоскостью проекции;
- плоскость V - фронтальной плоскостью проекции;
- плоскость W - профильной плоскостью проекции

Линии пересечения плоскостей проекции образуют оси координат:
- ось x - называют осью абсцисс;
- ось y - осью ординат;
- ось z - осью аппликат.
Точка пересечения координатных осей принимается за начало координат и обозначается буквой O (Origo - начало).

При этом положительным направлением осей координат считают:
- для оси x - от начала координат влево;
- для оси y - от плоскости V в сторону зрителя;
- ось z - от плоскости H вверх.
Противоположные направления осей считаются отрицательными.

Координатные плоскости делят пространство на восемь частей - октантов. Октанты условно принято нумеровать, так как это показано римскими цифрами на рисунке.
Каждый из октантов представляет прямоугольный трехгранник, у которого гранями служат части плоскостей проекций (называемых полами), а ребрами координатные оси.