Прямоугольная изометрия усеченной пирамидыПрямоугольная изометрия усеченной пирамиды строится с использованием приведенных коэффициентов искажений: kx = 1; ky = 1; kz = 1. Начинаем с построения сечения пирамиды плоскостью общего положения α в ортогональных проекциях. 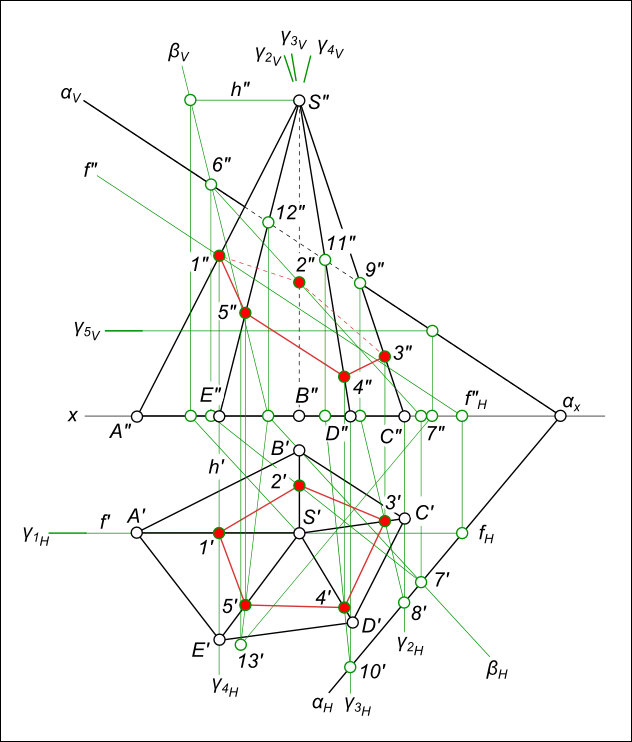 Прямоугольная изометрия усеченной пирамиды Оно уже выполнено,смотри статью: Сечение пирамиды плоскостью. Чертеж усеченной пирамиды взят оттуда.  Прямоугольная изометрия усеченной пирамиды Дальнейшие построение аксонометрической проекции Прямоугольная изометрия усеченной пирамиды выполняем по следующему графическому алгоритму: - Относим пирамиду к системе прямоугольных координат x, y и z, оси которой параллельны осям натуральной системы координат, и проходят через высоту пирамиды (ось z) и ее основание (оси x, y); - Определяем в принятой системе координат координаты x, y и z точек сечения 1(x1, y1, z1), 2(x2, y2, z2), 3(x3, y3, z3), 4(x4, y4, z4) и 5(x5, y5, z5) и точек A(xA, yA), B(xB, yB), C(xC, yC), D(xD, yD) и E(xE, yE) - вершин основания пирамиды; - На свободном месте чертежа начертить аксонометрические оси прямоугольной изометрии из произвольно взятой точки O: ось z - вертикально, оси x и y - под углом 120° к вертикальной линии; - Построить тонкими линиями аксонометрическую проекцию пирамиды: - построить аксонометрическое изображение основания пирамиды A0B0C0D0E0 по координатам этих точек; - построить по координате zS вершину пирамиды и соединить ее с вершинами основания - построив тем самым ребра пирамиды. - Построить сечение пирамиды - на ребрах пирамиды точки 1, 2, 3, 4 и 5 по соответствующим координатам: - точку 1 на ребре SA0 - по координатам x1, y1, z1; - точку 2 на ребре SB0 - по координатам x2, y2, z2; - точку 3 на ребре SC0 - по координатам x3, y3, z3; - точку 4 на ребре SD0 - по координатам x4, y4, z4; - точку 5 на ребре SE0 - по координатам x5, y5, z5. - Обвести аксонометрическое изображение пирамиды и ее сечения, выполнив основными линиями ее видимый контур, штриховыми линиями невидимые линии контура, штрихпунктирной линией высоту пирамиды, тонкими линиями полное изображение пирамиды и размерные линии. +
|
