Метод преобразованияМетод преобразования представляет собой переход от общего положения геометрической фигуры к частному, который можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости проекции двумя путями: во-первых, перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве. во-вторых, перемещением плоскостей проекций в новое положение, по отношению к которому проецируемая фигура (которая не меняет своего положения в пространстве) окажется в частном положении. Первый путь лежит в основе метода плоскопараллельного перемещения; второй составляет теоретическую базу метода перемены плоскостей проекций. В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений при этом определяются не только сложностью задачи, но и в значительной степени зависят от того с какими проекциями (удобными, неудобными) приходится иметь дело. Задачи решаются значительно проще в случае если используется метод преобразования общего положения геометрической фигуры относительно плоскости проекции к частному. Из приведенных ниже примеров проецирования прямоугольного треугольника видно, что вид проекции (ее форма и размеры) определяются не только формой и размерами проецируемой фигуры, но и в значительной степени зависит от взаимного расположения объекта проецирования и плоскости проекций. 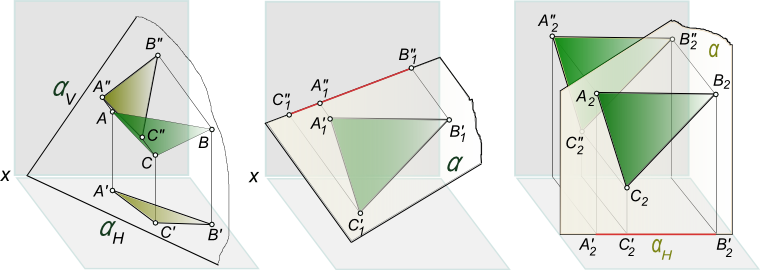 Метод преобразования Действительно, три конгруентных прямоугольных треугольника ΔABC≅ΔA1B1C1≅ΔA2B2C2 (рисунок) в зависимости от взаимного расположения плоскости треугольника и плоскости проекции V могут проецироваться на эту плоскость: а) в виде ΔA"B"C" = ΔABC, если плоскость треугольника занимает произвольное положение относительно плоскости V. ΔA"B"C" в метрическом отношении не имеет ничего общего с оригиналом - ΔABC (рисунок слева); б) в виде отрезка прямой [C"1B"1], в случае, когда плоскость ΔA1B1C1⊥V (рисунок в центре); в) либо в виде ΔA"2B"2C"2 ≅ ΔA2B2C2, когда плоскость ΔA2B2C2 ║ V (рисунок справа) Сопоставляя между собой оригинал и его ортогональную проекцию, мы видим, что только в случае параллельности проецируемой фигуры плоскости проекции возможно получить проекцию на эту плоскость, конгруентную самой фигуре, и, следовательно, полностью сохраняющую ее метрику. Форма и размеры фронтальной проекции ΔA"2B"2C"2 (рисунок справа) позволяют без каких либо построений ответить на вопросы: какова длина сторон треугольника, величина углов при вершинах, чему равна его площадь и другие метрические характеристики ΔA2B2C2. На рисунке показаны плоскость α, заданная двумя параллельными прямыми a и b, и пересекающая ее прямая m. 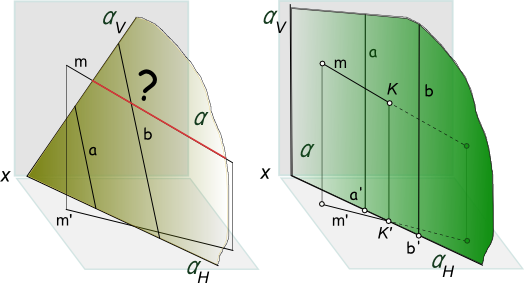 Метод преобразования На рисунке (слева) плоскость α общего положения. На рисунке справа плоскость α занимает проецирующее положение по отношению к горизонтальной плоскости проекции. Для определения точки K, в которой прямая m пересекает плоскость α, в случае показанном на рисунке слева необходимо выполнить дополнительные геометрические построения. В то же время, определение точки K на рисунке справа может быть выполнено непосредственно на чертеже (эпюре) без каких-либо дополнительных построений. Наиболее выгодным частным положением проецируемой фигуры следует считать: а) положение перпендикулярное к плоскости проекции (для решения позиционных, а в ряде случаев, и метрических задач); б) положение, параллельное по отношению к плоскости проекции (при решении метрических задач). +
|
