Взаимно перпендикулярные прямые

Взаимно перпендикулярные прямые, пересекаясь имеют одну общую точку и образуют при этом плоский угол.

Если проекция некоторого угла, у которого одна сторона, параллельна плоскости проекции, равна прямому углу, то и проецируемый угол также прямой.

Взаимно перпендикулярные прямые могут быть проведены на основе данного утверждения на эпюре Монжа: из двух пересекающихся под прямым углом прямых, необходимо чтобы одна из них была параллельна какой-либо плоскости проекции.

Через точку A провести прямую m перпендикулярную горизонтали h (на рисунке это отрезок [BC]) .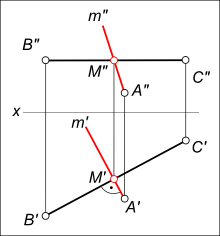

Взаимно перпендикулярные прямые

h` - это горизонтальная проекция прямой h параллельной плоскости проекции H. Принимая ее за одну сторону прямого угла, восстанавливаем из точки A` перпендикуляр m` и на их пересечении находим точку M`. По линии связи определяем недостающую проекцию M".

Через точку A провести прямую m ⊥[BC].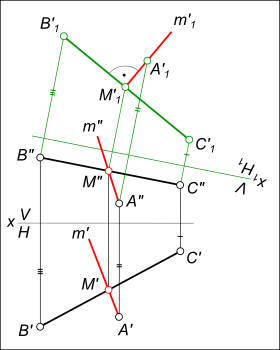

Взаимно перпендикулярные прямые

Судя по проекциям отрезка [B`C`], [B"C"], они принадлежат прямой [BC] общего положения. До того как опустить перпендикуляр из точки A на данную прямую, необходимо перевести ее в частное положение:
- [BC] ║ H, на эпюре: [B`C`] ║ x
или
- [BC] ║ V, на эпюре: [B"C"] ║ x.
Перевод осуществляем способом перемены плоскостей проекций - введя новую плоскость проекции H₁, проведя ось x₁ ║ [B"C"]. На H₁ строим проекции отрезка [B`<sub>1</sub>C`₁], которая представляет собой проекцию горизонтальной прямой и проекцию точки A`<sub>1</sub>. Из точки A`₁, опуская перпендикуляр к [B`<sub>1</sub>C`₁], находим точку M`<sub>1</sub> и далее M", M` и m", m`.

Провести недостающую горизонтальную проекцию стороны BC прямого угла ABC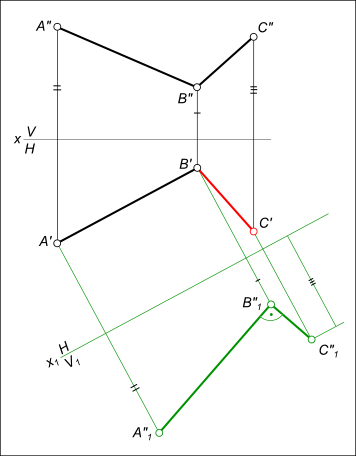

Взаимно перпендикулярные прямые