Найти угол между двумя плоскостями

Найти угол между двумя плоскостями - это значит определить линейный угол, образованный двумя прямыми - сечениями граней этого угла плоскостью, перпендикулярной к их ребру.
Угол между двумя плоскостями - это двугранный угол, гранями которого служат, пересекающиеся плоскости. Линию пересечения плоскостей называют ребром двугранного угла.

Для построения линейного угла, необходимо выполнить следующие графические построения в определенной последовательности: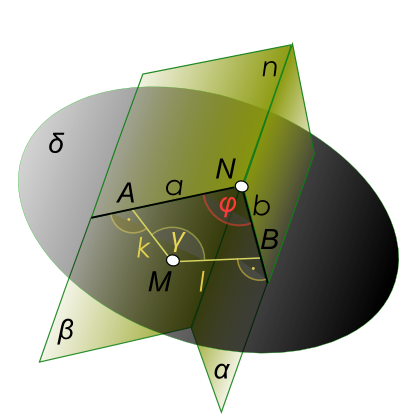

Найти угол между двумя плоскостями

- Определить прямую n - линию пересечения данных плоскостей α и β

- Провести плоскость δ ⊥ n (эта плоскость будет перпендикулярна также и к плоскостям α и β)

- Определить следы плоскости δ на плоскостях α и β

- Найти действительную величину ∠φ между прямыми a и b (следами). ∠ φ - искомый

Решение задачи - найти угол между двумя плоскостями - может быть упрощено построением:
- дополнительной точки M ∈ δ;
- перпендикуляров k и l опущенных из этой точки на прямые a и b (следы плоскости δ);
- точки A - пересечения k ∩ a;
- точки B - пересечения l ∩ b;
- точки N = a ∩ b.

В четырехугольнике MANB углы при вершинах A и B прямые. Следовательно, между углами при вершинах M и N существует зависимость, которую можно выразить равенством:

Теперь все решение сводится к построению ∠ γ путем проведения из произвольной точки пространства M прямых k и l, перпендикулярных к заданным плоскостям и определению ∠ γ между этими прямыми. После чего подсчитывается значение величины ∠ φ.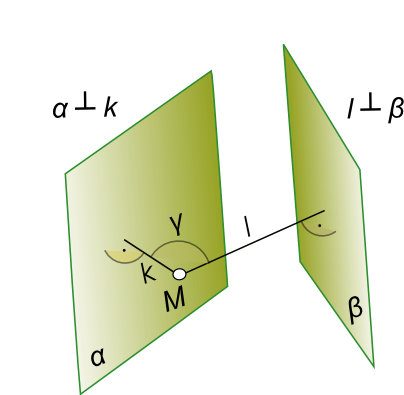

Найти угол между двумя плоскостями

Найти угол между двумя плоскостями:
плоскость α задана параллельными прямыми, а плоскость β - пересекающимися.

Найти угол между двумя плоскостями

Для определения действительной величины ∠ γ фигуры lMk может быть использован способ Вращение вокруг горизонтали или фронтали . Затем вычисляем ∠φ = 180° - ∠γ.

Другие графические способы определение действительной или натуральной величины угла между плоскостями или гранями основаны на методах изложеных в статье:
Метод преобразования