Найти угол между прямой и плоскостью

Найти угол между прямой и плоскостью - это означает найти угол между этой прямой и ее проекцией на данную плоскость.

Пространственная модель иллюстрирующая задачу найти угол между прямой и плоскостью представлена на рисунке.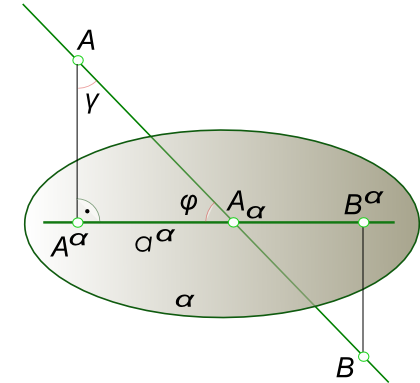

Найти угол между прямой и плоскостью

План решения задачи:
1. Из произвольной точки A∈a опускаем перпендикуляр на плоскость α;
2. Определим точку встречи этого перпендикуляра с плоскостью α. Точка A_α - ортогональная проекция A на плоскость α;
3. Находим точку пересечения прямой a с плоскостью α. Точка a^α - след прямой a на плоскости α;
4. Проводим (A^αa^α) - проекцию прямой a на плоскость α;
5. Определяем действительную величину ∠Aa_αA^α, т. е. ∠φ.

Решение задачи найти угол между прямой и плоскостью может быть значительно упрощено, если определять не ∠φ между прямой и плоскостью, а дополняющий до 90° ∠γ. В этом случае отпадает необходимость в определении проекции точки A и проекции прямой a на плоскость α. Зная величину γ, вычисляем по формуле:

Определение угла между прямой a и плоскостью α, заданной параллельными прямыми m и n.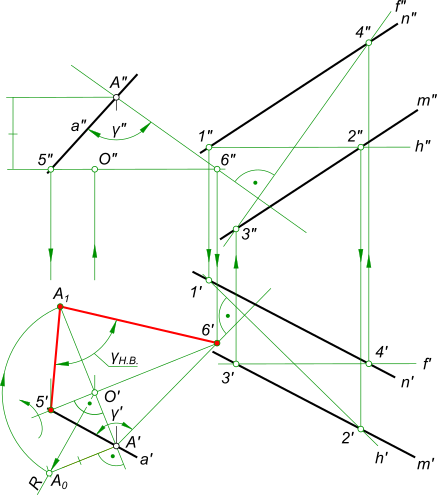

Найти угол между прямой и плоскостью

Из произвольной точки на прямой a опускаем перпендикуляр к плоскости α
Вращением вокруг горизонтали заданной точками 5 и 6 определяем натуральную величину ∠γ. Зная величину γ, вычисляем по формуле:

Определение угла между прямой a и плоскостью α, заданной треугольником BCD.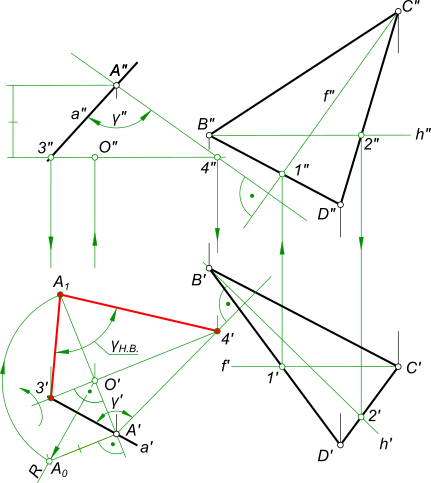

Найти угол между прямой и плоскостью

Из произвольной точки на прямой a опускаем перпендикуляр к плоскости α
Вращением вокруг горизонтали заданной точками 3 и 4 определяем натуральную величину ∠γ. Зная величину γ, вычисляем по формуле:

Определение угла между прямой a и плоскостью α, заданной следами.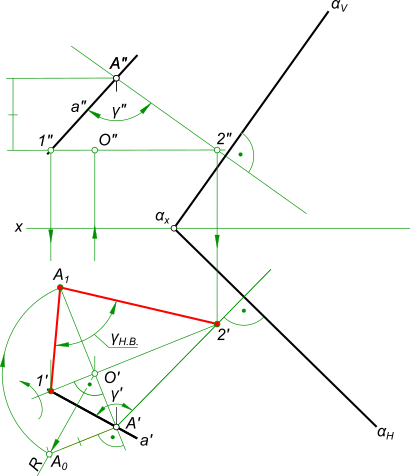

Найти угол между прямой и плоскостью

Из произвольной точки на прямой a опускаем перпендикуляр к плоскости α
Вращением вокруг горизонтали заданной точками 1 и 2 определяем натуральную величину ∠γ. Зная величину γ, вычисляем по формуле: