Определение величины отрезка

Определение величины отрезка или расстояния между двумя точками прямой - эта задача возникает, когда отрезок прямой занимает общее положение.
Эта же задача может быть выражена по другому - найти расстояние между двумя точками прямой.
Ортогональная проекция отрезка прямой на плоскость H (V или W) конгруентна оригиналу лишь в том случае, когда он параллелен плоскости H (V или W).

Аналогично:

Во всех остальных случаях он проецируется на плоскость проекции с искажением. При этом ортогональная проекция отрезка всегда будет меньше его действительной величины.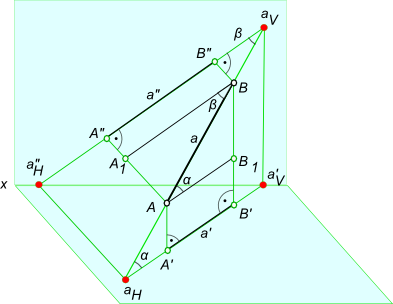

Определение величины отрезка

Определение величины отрезка на эпюре Монжа заключается в построении прямоугольного треугольника - взяв за один его катет горизонтальную (фронтальную, профильную) проекцию отрезка, а за другой катет - разность удаления концов отрезка от горизонтальной (или соответственно фронтальной, профильной) плоскости проекции.

Графическое определение расстояния между двумя точками прямой [AB] или действительной величины отрезка [AB] путем построения прямоугольного треугольника - ΔA`B`B₀ или прямоугольного треугольника - ΔA"B"A₀.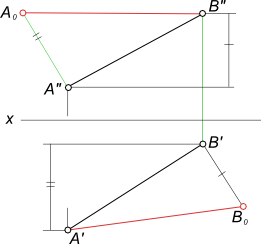

Определение величины отрезка

С помощью прямоугольного треугольника можно решать задачу по построению на эпюре:
- проекции отрезка, наперед заданной величины;
- расстояния между двумя точками прямой, наперед заданной величины.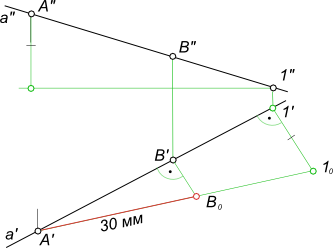

Определение величины отрезка

Определение величины отрезка или расстояния между двумя точками прямой путем вращения вокруг оси ⊥ H (i ∋ B).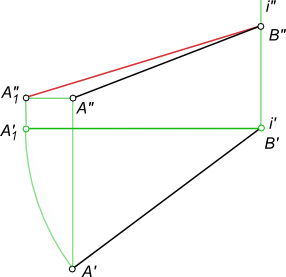

Определение величины отрезка

Определение величины отрезка применяется в статье графическая работа 1: Графическая работа 1