Признаки параллельности плоскостей

Признаки параллельности плоскостей имеет следующее определение: две произвольные пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

В проективном пространстве две плоскости пересекаются по прямой - собственной или несобственной. Во втором случае плоскости принято называть параллельными.

Используя признаки параллельности плоскостей, можно получить простой графический способ решения задачи по построению плоскости, параллельной заданной.

Провести через точку K плоскость β параллельную плоскости α(a║b)

Признаки параллельности плоскостей

Алгоритм решения задачи:
- для построения плоскости β мы вправе, взять одну прямую m(m`, m") из пересекающихся прямых, проходящих через точку K(K`, K") и параллельных плоскости α - например параллельной прямым a и b.
- согласно же условию параллельности плоскостей, в плоскости α необходимо иметь пересекающиеся прямые. Для этого строим прямую 1-2.
- далее проводим через точку K(K`, K") вторую из пересекащихся прямых плоскости β - прямую n(n`, n") параллельно прямой 1-2.

Провести через точку K плоскость β параллельную данной плоскости α, выразив ее следами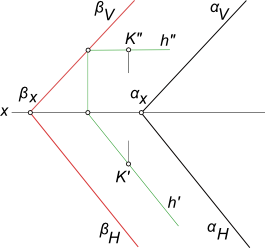

Признаки параллельности плоскостей

Здесь следы плоскости βH и βV- это две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым αH и αV заданной плоскости α.

Провести через точку S плоскость α параллельную плоскости треугольника ABC, выразив ее следами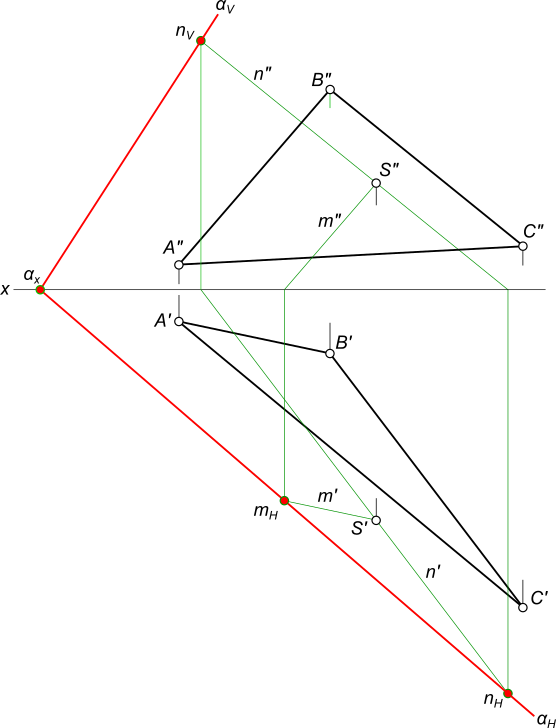

Признаки параллельности плоскостей

Здесь следы плоскости αH и αV построены по следам двух прямым m и n, пересекающихся в точке S и при этом параллельных сторонам AB и BC треугольника соответственно.