Признаки параллельности прямой и плоскости

Признаки параллельности прямой и плоскости имеют следующее определение - прямая m параллельна плоскости α, если в плоскости α можно провести прямую n, параллельную m:

Очевидно через точку пространства, не принадлежащую плоскости, можно провести бесчисленное множество прямых, параллельных данной плоскости.

Через точку A провести прямую m, параллельную плоскости α, заданной пересекающимися прямыми a и b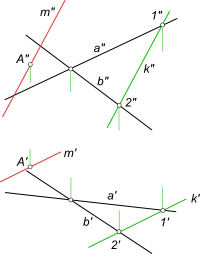

Признаки параллельности прямой и плоскости

Если нет никаких дополнительных условий, то мы вправе, используя признаки параллельности прямой и плоскости, провести любую прямую из множества прямых, проходящих через точку A и параллельных плоскости α - например параллельно одной из прямых a или b. Если же поставлено условие, чтобы прямая не была параллельна прямым a и b - необходимо построить прямую 12 и провести искомую прямую m(m`, m") параллельно ей.

Через заданную точку A провести плоскость, параллельную прямой f

Признаки параллельности прямой и плоскости

Плоскость задаем пересекающимися в точке A прямыми a и b. При этом одна из прямых (прямая a) параллельна прямой f.

Через заданную точку K провести прямую, параллельную плоскости треугольника ABC и фронтали, проходящей через вершину A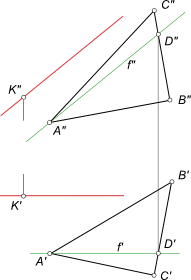

Признаки параллельности прямой и плоскости

Построим фронталь f по заданному условию: - через точку A` параллельно оси x проводим прямую f`. Данная прямая пересекает B`C` - сторону треугольника в точке D`. По линии связи находим фронтальную проекцию D" точки D, принадлежащей стороне BC треугольника. Проводим через точки A" и D" прямую f". Через точку K проводим прямую параллельную фронтали f. Данная прямая будет параллельна и плоскости треугольника ABC.

Через точку A(-3;4;-3) провести прямую параллельную двум плоскостям α(3x+4y-2z+7=0) и β(x-2z+5=0)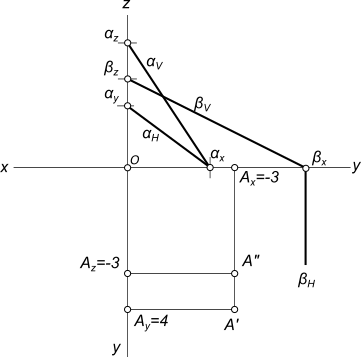

Признаки параллельности прямой и плоскости

1. Строим проекции точки A
2. Строим следы плоскости α (3x+4y-2z+7=0):
a) z=0; 3x+4y+7=0;
αH; y=0; 3x+7=0, x=-7/3, x=-2,33;
b) y=0; 3x-2z+7=0;
αV; x=0; -2z+7=0, z=3,5;
z=0; 3x+7=0, x=-2,33
3) Строим следы плоскости β (x-2z+5=0):
βV x=0; -2z+5=0, z=5/2, z=2,5;
z=0; x+5=0, x=-5
4) Строим линию пересечения 1—2 заданных плоскостей α и β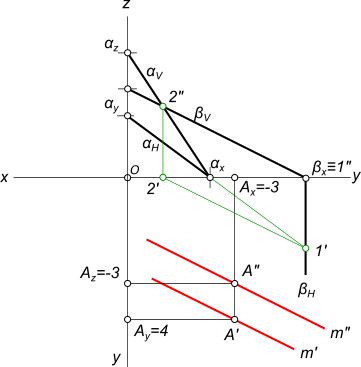

Признаки параллельности прямой и плоскости

5) Строим линию m параллельную плоскостям α и β:
m`‖1`—2` и m"‖1"—2"