Признаки параллельности прямыхПризнаки параллельности прямых, и правило для построения на эпюре Монжа параллельных прямых вытекают из четвертого свойства параллельного проецирования - если в пространстве прямые параллельны, то их одноименные проекции также параллельны между собой.
\[
(∀ a,b)(a ║ b)⇒[(a` ║ b`) ∧ (a" ║ b") ∧ (a"` ║ b"`)]
\]
Причем, если в пространстве прямые a и b занимает общее положение относительно плоскостей проекций, то для выяснения по эпюру вопроса о соответствии их определению признаки параллельности прямых достаточно убедится, будут ли параллельны между собой их одноименные проекции только на двух плоскостях. Параллельность проекции на третьей плоскости в этом случае автоматически удовлетворяется. 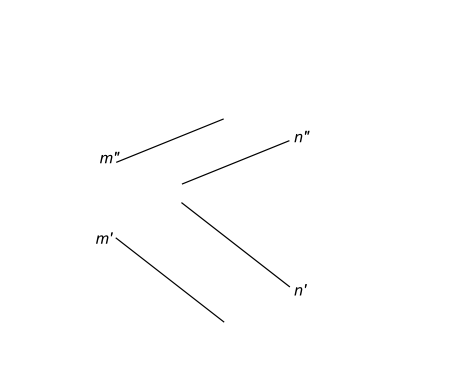 Признаки параллельности прямых [(a`║b`)∧(a"║b")]∧(a"`║b"`) Следовательно, по условию, a║b. Прямые AB и CD параллельны 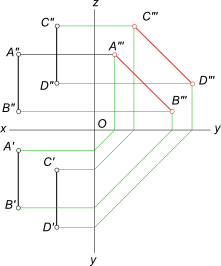 Признаки параллельности прямых Прямые EF и KL не параллельны 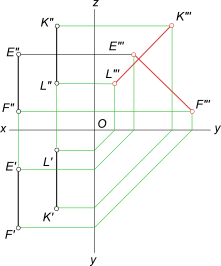 Признаки параллельности прямых +
|
РазделыПроекции плоских угловВеличина плоского углаВзаимно перпендикулярныеНайти угол междуПризнаки параллельностиНатуральная величина треугольникаОпределение величины отрезкаРасстояние между точкой и прямойРасстояние между двумя параллельными прямымиРасстояние между точкой и плоскостьюРасстояние между двумя плоскостямиРасстояние между скрещивающимися прямымиСпособ прямоугольного треугольникаУглы наклона прямойУгол между скрещивающимися прямыми
href="http://ngeo.fxyz.ru/" title="Начертательная геометрия"> <img src="http://ngeo.fxyz.ru/data/img/ngeo-88x31.png" alt="Начертательная геометрия" /> </a> |
