Проекции плоских углов

Свойства ортогональных проекций плоских углов:

1. Если стороны угла не параллельны плоскости проекции, то угол проецируется на эту плоскость с искажением.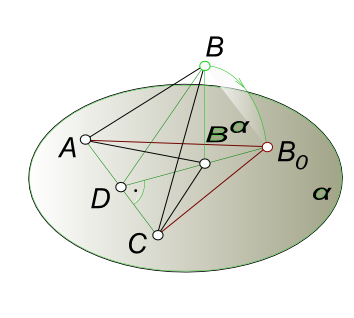

Проекции плоских углов

Пусть стороны AB и BC ∠ABC равнонаклонены к плоскости α

∠AB^αC - проекция ∠ABC на плоскость α. Совместим ∠ABC с плоскостью α путем вращения вокруг (AC)⊂α.

В этом случае ∠AB^αC окажется внутри ∠AB₀C, а их вершины B^α и B₀ на одной прямой (DB₀⊥AC). Следовательно,

∠AB^αC ≠ ∠AB₀C

2. Если хотя бы одна сторона тупого, прямого или острого угла параллельна плоскости проекции, то проекцией угла на эту плоскость будет угол с тем же названием, что и сам угол (тупой, прямой, острый).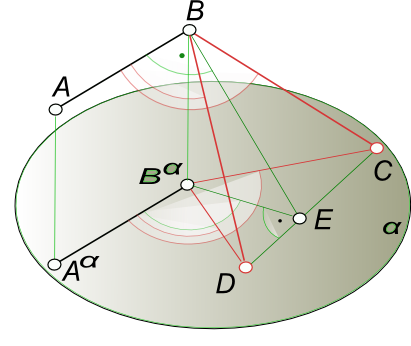

Проекции плоских углов

[AB]║α. Строим тупой ∠ABC и острый ∠ABD. Сторону BD угла ∠ABD проводим так, чтобы [BD] принадлежал плоскости, определяемой точками A, B, C [BD]⊂(A, B, C).

Проводим в плоскости (A, B, C), [BE]⊥[AB]. Так как ∠ABE прямой, а сторона угла [AB]║α, то проекция этого угла на плоскость α также будет равна 90°.

[(∠ABC = 90°)]∧[AB]║α]⇒∠A^αB^αE = 90°

Из чертежа видно, что ∠A^αB^αD < 90°, ∠A^αB_αC > 90°. при этом:

а) проекция острого угла будет меньше проецируемого угла.

б) прямой угол проецируется без искажений.

в) проекция тупого угла больше проецируемого угла.

Если проекция некоторого угла, у которого одна сторона, параллельная плоскости проекции, равна прямому углу, то и проецируемый угол также прямой.

3. Если обе стороны любого угла параллельны плоскости проекции, то угол проецируется на эту плоскость без искажения.

4. Проекции острого и тупого углов могут проецироваться на плоскость проекции без искажения не только при условии параллельности сторон угла плоскости проекции.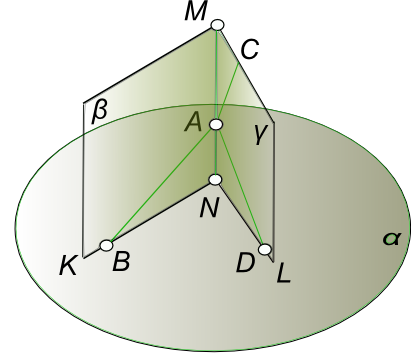

Проекции плоских углов

Из чертежа видно, что все углы с вершиной на прямой (MN), стороны которых расположены в проецирующих плоскостях β и γ, проецируются в ∠KNL; при этом проецируемые углы ∠BAD и ∠BAC могут изменяться в пределах от 0 до 180°. Естественно среди них будет угол, равный ∠KNL.

5. Если стороны угла параллельны плоскости проекции или одинаково наклонены к ней, то деление пополам проекции угла соответствует его делению пополам в пространстве.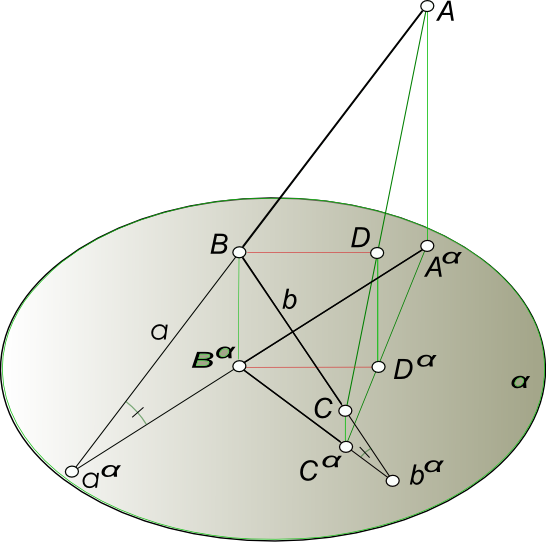

Проекции плоских углов

Стороны ∠ABC наклонены под одинаковым углом к плоскости проекции α: ∠Aa_αA^α = ∠Bb_αB^α. ∠A^αB^αC^α - ортогональная проекция ∠ABC на плоскость α. [B^αD^α) - биссектриса ∠A^αB^αC^α. На основании свойств биссектрисы внутреннего угла в треугольнике

Но по свойству инвариантного проецирования - если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией этой точки в том же отношении.

Следовательно,

но │B^αA^α│ = │BA│cos ∠Aa_αA^α и │B^αC^α│ = │BC│cos ∠Bb_αB^α, откуда

Следовательно

т. е.

[BD) - биссектриса ∠ABC.