Расстояние между двумя параллельными прямыми

Расстояние между двумя параллельными прямыми, определяется величиной перпендикуляра, опущенного из точки, взятой на одной прямой, на другую прямую.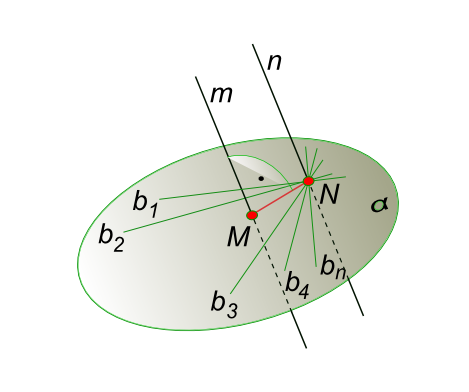

Расстояние между двумя параллельными прямыми

На основе данного определения составляем алгоритм решения задачи в общем виде:
- берем произвольную точку N на одной прямой;
- из точки N опускаем перпендикуляр на на другую прямую:
- через точку N проводим плоскость α перпендикулярную параллельным прямым n и m.
- находим точку встречи M прямой m с плоскостью α;
- соединяем точки N и M отрезком прямой;
- определяем действительную величину отрезка [NM} способом прямоугольного треугольника.
Расстояние между двумя параллельными прямыми определяется путем реализации данного алгоритма графических построений.

Решение задачи на расстояние между двумя параллельными прямыми значительно упрощается, если прямые будут параллельны плоскости проекции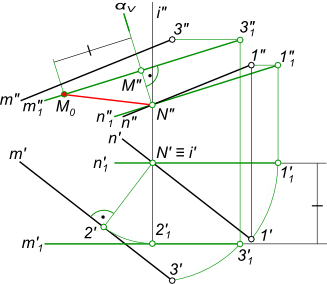

Расстояние между двумя параллельными прямыми

Ход решения:
- на прямой n отмечаем произвольную точку N;
- вращаем прямые m и n вокруг оси i ⊥ H (i ∋ N) до положения ║ V. Проекции прямых (n`<sub>1</sub> ║ оси x) и (m`₁ ║ оси x) - переведены в частное положение способом вращения вокруг оси перпендикулярной плоскости проекций H;
- из точки N" опускаем перпендикуляр (N"M") на прямую m"₁. Определяем действительную величину [MN] способом прямоугольного треугольника.

Решение задачи на расстояние между двумя параллельными прямыми способом плоскопараллельного перемещения: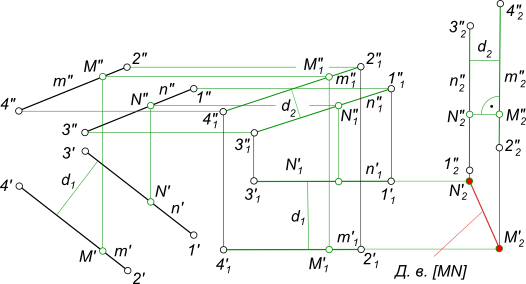

Расстояние между двумя параллельными прямыми

- первым шагом прямые переводятся в частное положение - положение фронтальных прямых, при этом перемещении d₁ = const, (m` ║ n`) ║ оси x;
- вторым шагом прямые переводятся в частное положение - положение горизонтально-проецирующих прямых, при этом перемещении d₂ = const, (m" ║ n") ⊥ оси x;
- проекциями горизонтально-проецирующих прямых n"₂ и m"₂ будут точки N`<sub>2</sub> и M`₂, соединив которые прямой линией получим отрезок [N`<sub>2</sub>M`₂] - соответствующий действительной величине расстояния между двумя параллельными прямыми m и n.
Обратным проецированием точки N и M могут быть построены на исходных проекциях.