Расстояние между двумя плоскостями

Расстояние между двумя плоскостями определяется величиной отрезка перпендикуляра, опущенного из точки взятой на одной плоскости, на другую плоскость.

Исходя из этого определения может быть составлен алгоритм из следующих элементарных задач, выполняемых в порядке очередности:
- взять в плоскости α произвольную точку A (A ∈ α);
- из точки A опустить перпендикуляр m на плоскость β (m ∋ A) ∧ (m ⊥ β);
- найти точку M пересечения перпендикуляра m с плоскостью β (M = m ∩ β);
- определить действительную величину [AM] (d = │ AM │).

Задачи на расстояние между двумя плоскостями решаются путем реализации этого алгоритма графических построений. Задача значительно упрощается, если параллельные плоскости перевести в частное положение (проецирующее) по отношению к плоскостям проекций.

В качестве примера решаем задачу на расстояние между двумя плоскостями заданными следами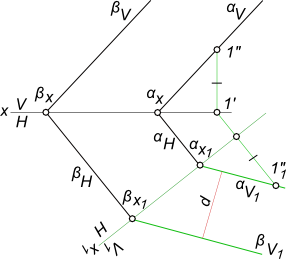

Расстояние между двумя плоскостями

определяем способом перемены плоскостей проекций

Провести плоскость β ║ α, на расстоянии равном d. Плоскость α задана параллельными прямыми.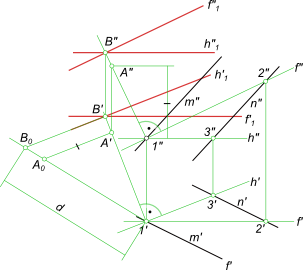

Расстояние между двумя плоскостями

Расстояние между двумя плоскостями d, заданное условием задачи, строим используя способ прямоугольного треугольника.

Для восстановления ┴ к заданной плоскости, проводим в ней пересекающиеся в точке 1 горизонталь h и фронталь f. Из точек 1` и 1" проводим направления 1`A` и 1"A" перпендикулярные h` и f" соответственно. Искомую плоскость задаем пересекающимися прямыми горизонталью h₁ и фронталью f₁.

Построение плоскости параллельной заданной выполнено в графической работе №2:
Графическая работа 2,
где Расстояние между двумя плоскостями d, заданное условием задачи, строится с использованием способа прямоугольного треугольника.