Расстояние между точкой и плоскостью

Расстояние между точкой и плоскостью определяется величиной отрезка перпендикуляра, опущенного из точки на плоскость.

Решение задачи на расстояние между точкой и плоскостью состоит из последовательного выполнения следующих графических построений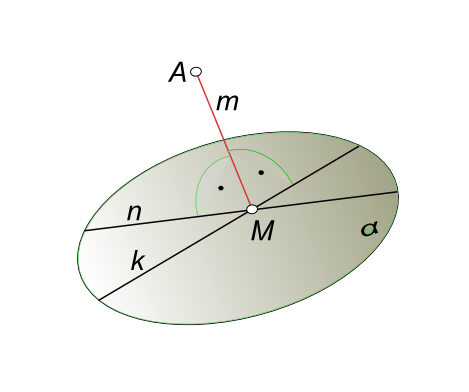

Расстояние между точкой и плоскостью

- из точки A опустить перпендикуляр m на плоскость α
(m ∋ A) ∧ (m ⊥ α);
- найти точку M пересечения этого перпендикуляра с плоскостью α
M = m ∩ α;
- определить действительную величину [AM].

Если плоскость α общего положения, то для того чтобы опустить на эту плоскость перпендикуляр, необходимо предварительно определить направление проекций горизонтали и фронтали этой плоскости. Нахождение точки встречи этого перпендикуляра с плоскостью также требует выполнения дополнительных графических построений.
Решение задачи упрощается, если плоскость α будет занимать частное положение по отношению к плоскостям проекций.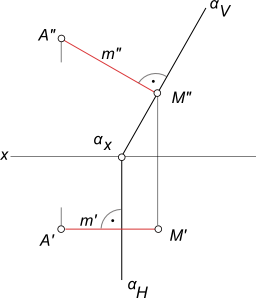

Расстояние между точкой и плоскостью

Расстояние между точкой и плоскостью определяется без каких-либо дополнительных построений, т. к. плоскость α занимает фронтально-проецирующее положение.

Расстояние между точкой и плоскостью заданной ΔABC определяется способом перемены плоскостей проекций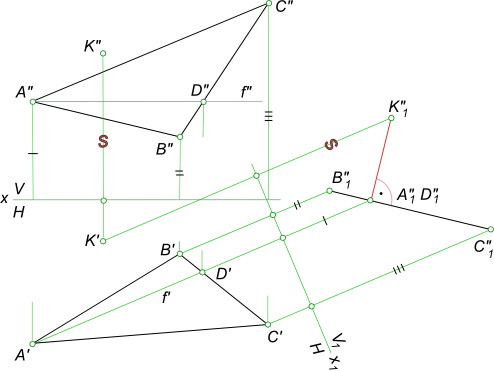

Расстояние между точкой и плоскостью

Расстояние между точкой и плоскостью α заданной заданной следами определяется способом перемены плоскостей проекций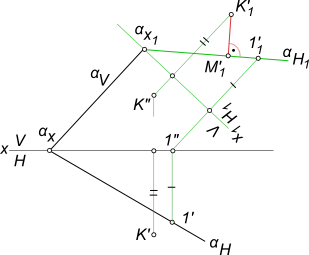

Расстояние между точкой и плоскостью

Расстояние между точкой и плоскостью α заданной заданной ΔABC определяется классическим методом или способом прямоугольного треугольника в графической работе 2: Графическая работа 2