Углы наклона прямой

Углы наклона прямой общего положения по двум ее проекциям находятся попутно при определении действительной величины отрезка способом прямоугольного треугольника. В отличие от отрезков прямых частного положения, проецирующихся хотя бы на одну из плоскостей проекций в натуральную величину, отрезок прямой общего положения на плоскости проекций проецируется с искажением. Для того чтобы найти его натуральную величину, необходимо провести ряд преобразований.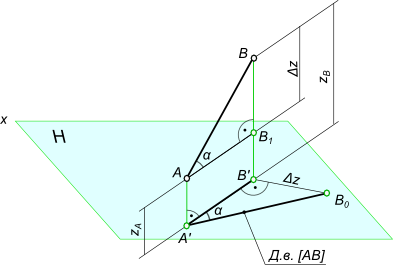

Углы наклона прямой

Возьмем прямую общего положения АВ и спроецируем ее на горизонтальную плоскость проекций . Через точку А проведем линию, параллельную плоскости . Таким образом в пространстве получим прямоугольный треугольник , один из катетов которого (AB₁) равен длине проекции отрезка, а угол между отрезком и этим катетом является углом наклона заданного отрезка к плоскости проекций (рис.).

Для определения натуральной величины отрезка прямой общего положения и угла наклона ее к плоскости проекций на эпюре (КЧ) необходимо построить прямоугольный треугольник:
- первый катет этого треугольника равен проекции отрезка на плоскости проекций (обычно прямоугольный треугольник пристраивают к проекции отрезка, однако в некоторых задачах целесообразно прямоугольный треугольник строить в стороне от проекций геометрических объектов);
- из проекции любого конца отрезка под прямым углом к проекции отрезка проводится луч, на котором откладывается длина второго катета, равная разности расстояний от концов отрезка до данной плоскости проекций;
- гипотенуза полученного таким образом прямоугольного треугольника равна действительной величине заданного отрезка;
- угол наклона отрезка к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией на эту плоскость проекций.

Углы наклона прямой, отрезка общего положения всегда будут меньше их ортогональных проекций.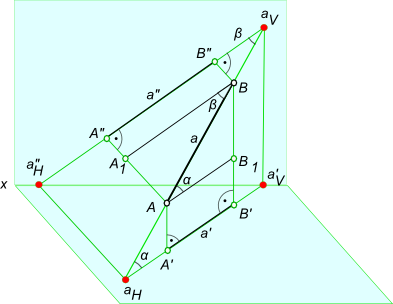

Углы наклона прямой

Для графического определения на эпюре Монжа действительной величины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную (фронтальную, профильную) проекцию отрезка, а за другой катет - разность удаления концов отрезка от горизонтальной (или соответственно фронтальной, профильной) плоскости проекции.

Графическое определение действительной величины отрезка [AB] путем построения прямоугольных треугольников ΔA`B`B₀ или ΔA"B"A₀ и попутно углов его наклона:
- α к горизонтальной плоскости проекции;
- β к фронтальной плоскости проекции.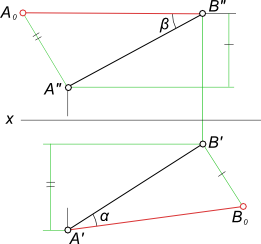

Углы наклона прямой

Углы наклона прямой к плоскости проекций проецируется на эпюре без искажений, когда она занимает положение прямой уровня, это может быть:
- Горизонтальная прямая;
- Фронтальная прямая;
- Профильная прямая

Углы наклона прямой применяются в статье графическая работа 1: Графическая работа 1

Определение углов наклона плоскости смотри также: Линия наибольшего наклона