Взаимное положение прямых

Взаимное положение прямых в проекциях с числовыми отметками может быть:
- параллельным;
- пересекающимся;
- скрещивающимся.
Чтобы определить взаимное положение прямых в проекциях с числовыми отметками, достаточно спроецировать их на какую-либо горизонтально проецирующую плоскость и затем совместить эту плоскость с горизонтальной плоскостью проекций П1,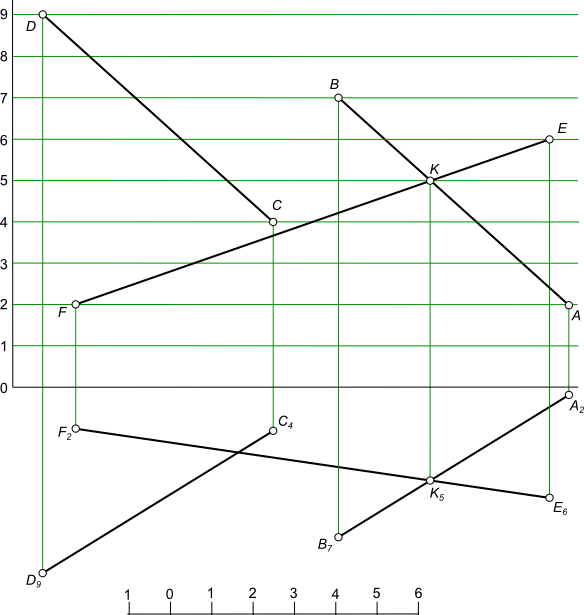

Взаимное положение прямых

что означает приведение чертежа к комплексному.
Для того чтобы задать параллельные прямые в проекциях с числовыми отметками, необходимо, чтобы проекции их были параллельны, интервалы или уклоны равны, отметки возрастали в одном направлении.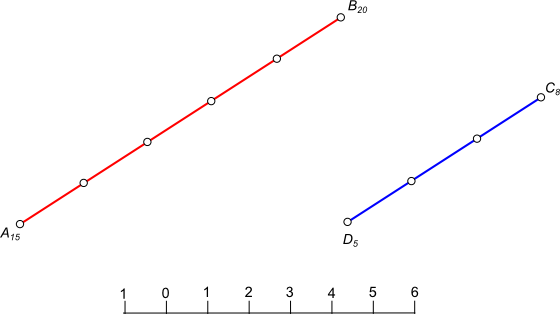

Взаимное положение прямых

Параллельные прямые в проекциях с числовыми отметками могут быть заданы при помощи двух начальных точек А15 и В20, направлением прямых и уклоном, который должен быть одинаковым для обеих прямых.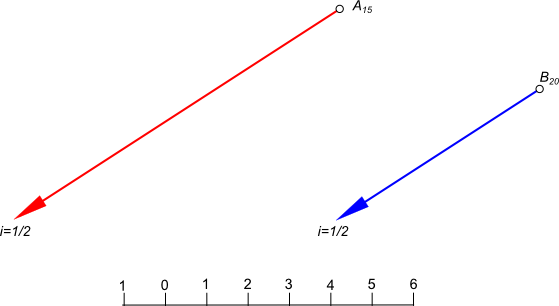

Взаимное положение прямых

Пересекающиеся прямые в проекциях с числовыми отметками достаточно спроецировать на какую-либо горизонтально проецирующую плоскость и затем совместить эту плоскость с горизонтальной плоскостью проекций П1. Проекции этих прямых также пересекаются, а проекции точки пересечения лежат на одном перпендикуляре к оси проекций Ох.
Пересекающиеся прямые имеют общую точку В8.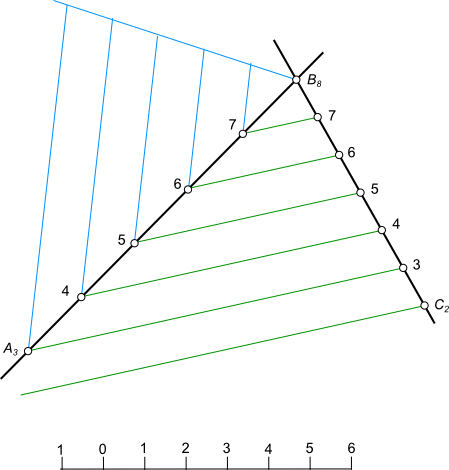

Взаимное положение прямых

В проекциях с числовыми отметками, чтобы определить пересекающиеся ли это прямые или нет, необходимо, проградуировать прямые, и если в точке пересечения прямые будут иметь одну и ту же отметку, то прямые пересекаются. Если в точке пересечения прямых их отметки разные, то прямые скрещивающиеся.
Если линии соединяющие точки с одинаковыми отметками на прямых параллельны между собой, то прямые пересекаются, в противном случае - скрещиваются.