Положение точки на прямой

Положение точки на прямой в проекциях с числовыми отметками.
Прямая A5B10, расположенная в пространстве, на чертеже имеет проекцию - прямую линию, которая соединяет проекцию точки A - A5 и проекцию точки B - B10. Чтобы на отрезке прямой A5B10 найти точку, имеющую отметку например 7 или 8, отрезок делят на разность отметок 10 - 5 = 5. это делается на основании того, что проекции прямой делятся в том же отношении, что и сама прямая в пространстве. Разделив отрезок AB на пять равных частей, получим проекции точек, имеющих отметки 6, 7, 8 и 9.
Для того чтобы получить точки с отметками например 6,5 или 9,5 надо отрезок разделить на 10 равных частей.

Если отметки отрезка прямой заданы не целыми числами, например A2,4B8,5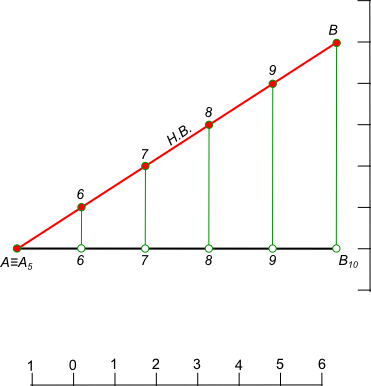

Положение точки на прямой

то для нахождения промежуточных точек с разностью в единицу проецируют отрезок на на вспомогательную вертикальную плоскость, расположенную параллельно проекции, и принимают ось проекции за нулевой уровень или за любой другой. Затем эту плоскость совмещают с горизонтальной плоскостью проекций.
Процесс нахождения точек, отметки которых выражены в целых числах с разностью в одну единицу, называется градуированием. Положение точки на прямой может быть найдено при помощи градуирования для любой точки прямой.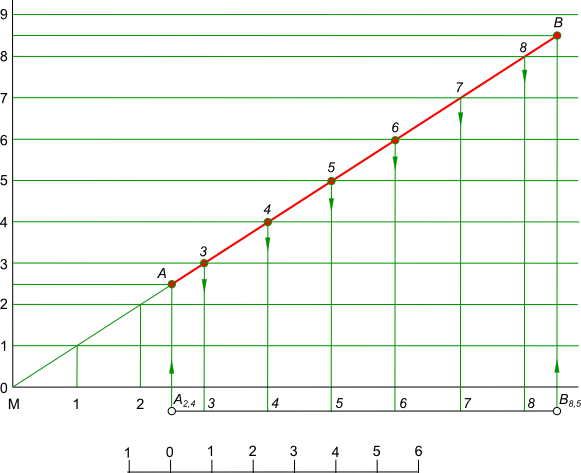

Положение точки на прямой

Построение заключается в следующем: - на расстоянии, равном масштабной единице расстояния, проводят ряд ппараллельных прямых, соответствующих уровням в 2...9 единиц - линии уровня;
- из проекций точек A2,4 и B8,5 восстанавливают перпендикуляры и на них находятуровень в 2,4 и 8,5 единиц между соответствующими линиями уровня;
- полученные точки соединяют прямой линией AB, которая пересечет все линии уровня в соответствующих точках 3...8;
- проведя линии связи из точек 3...8 на проекции прямой AB, находят проекции точек, отметки которых выражены целыми числами с разностью в одну единицу и расположены на равном расстоянии друг от друга.