Образование резьбы

Образование резьбы связано с использованием прямого и наклонного геликоидов изложенных в статье Винтовая поверхность.
Для описания резьбы применяют следующие ее характеристики:
- Профиль резьбы - это плоская фигура, полученная сечением витка резьбы осевой плоскостью. В зависимости от формы профиля различают резьбы треугольные, прямоугольные, трапецеидальные, круглые и т. п.
Правая однозаходная резьба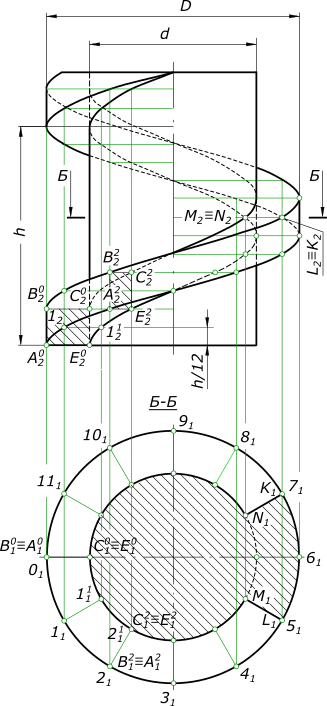

Образование резьбы

Образование резьбы однозаходной происходит в результате винтового движения одного профиля. Если производящими являются два профиля, получается двухзаходная резьба, например трапецеидальная резьба Если производящими являются три профиля, получается трехзаходная резьба и т. д.
У многозаходных резьб различают шаг резьбы и ход резьбы;
- Шаг резьбы - это измеренное вдоль образующей между двумя смежными витками, обозначается буквой s;
- Ходом резьбы называют расстояние, измеренное вдоль образующей между двумя точками одного и того же витка, и обозначают его буквой h.
Для многозаходных резьб h=2s например. У однозаходных резьб шаг s равен ходу h.
Данными для построения служат наружный и внутренний диаметры резьбы д и Д, производящий профиль резьбы - прямоугольник абсе и шаг резьбы эс.
Совершая поступательное и вращательное движение относительно оси винта, профиль резьбы опишет винтовой выступ, ограниченный двумя прямыми геликоидами и цилиндрической поверхностью.
Образование резьбы треугольного профиля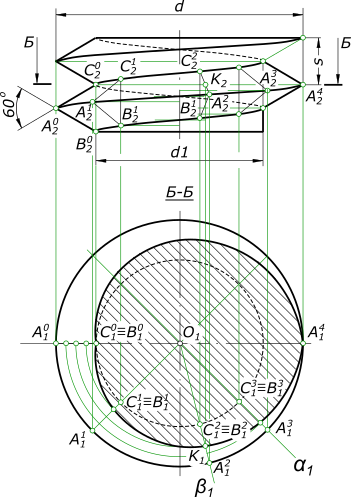

Образование резьбы

происходит в результате винтового движения производящего профиля - треугольника ABC(A2⁰B2⁰C2⁰), примыкающего к образующей цилиндра диаметра d1, стороной BC(B2⁰C2⁰). Данными для построения служат наружный и внутренний диаметры резьбы d и d1, производящий профиль резьбы - треугольник ABC и шаг резьбы s.
Совершая поступательное и вращательное движение относительно оси винта, профиль резьбы опишет винтовой выступ, ограниченный двумя наклонными геликоидами. Прямые AB и AC при своем движении, пересекая ось винта под углом 60°, образуют наклонные геликоиды, ограничивающие витки резьбы, описываемые точками A,B и C. Построение витка треугольной резьбы:
- выполняем построение винтовых линий описываемых точками A,B и C;
- выполняем построение сечения винта плоскостью Б - Б:
- поверхность наклонного геликоида рассеченная плоскостью перпендикулярной к его оси, дает на поверхности кривую - спираль Архимеда;
- для построения точек спирали рассекаем виток радиальными плоскостями α1, β1 и т. д.;
- строим для каждой секущей плоскости фронтальные проекции сечений витка - треугольники A2³B2³C2³, A2²B2²C2² и т. д.;
- плоскость Б - Б пересекает стороны A2³C2³ и A2²C2² и т. д. в точках M(M2), K(K2) и т. д. Строим их горизонтюльные проекции M1, K1 и т. д.;
- полученные точки соединяем плавной кривой.
Сечение Б - Б ограничено двумя ветвями архимедовой спирали - правого и левого ходов. При этом точка C(C1⁰, C2⁰) расположилась на образующей диаметра d1, а точка A(A1, A2) - на образующей диаметра d.
Получение точек M(M1), L(L1) и т. д. можно упростить, используя общепринятый способ построения спирали Архимеда.

Образование резьбы правого двухзаходного винта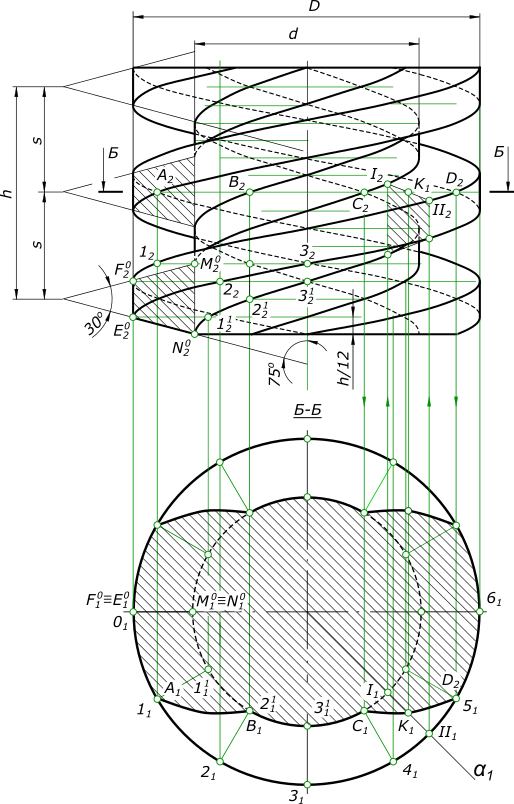

Образование резьбы

движением двуух одинаковых производящих профилей, имеющих форму равнобочной трапеции EFMN. При этом ее стороны FM и EN пересекают ось винта под углом 75°. Эти стороны при своем движении образуют наклонные геликоиды, а сторона EF образует цилиндрическую поверхность.
Для построения витков винта нужно предварительно построить винтовые линии, образуемые точками E, F, M и N.
Затем строим сечение винта плоскостью Б-Б. Эта плоскость рассекает винт по спиралям Архимеда и дугам окружностей. Так, кривая между точками B и C и ей симметричная являются дугами окружности радиуса d1/2, а кривая CK5 и ей симметричная - спиралями Архимеда.
Точки B и C находятся на боковой поверхности цилиндра диаметра d1 в точках пересечения плоскости Б-Б с винтовыми линиями, описанными этими точками.
Точка D находится на пересечении плоскости Б-Б с винтовой линией, описанной точкой F на боковой поверхности цилиндра.
Точки C и D принадлежат спирали Архимеда. Для построения промежуточных ее точек, например, точки К проводим радиальную плоскость α(α1). Эта плоскость пересечет виток по трапеции. Одна из сторон трапеции - отрезок 1-II. Точка пересечения плоскости Б-Б с этим отрезком дает промежуточную точку К.