Построение аксонометрических проекций окружностиПостроение аксонометрических проекций окружности вызывает трудности, в связи с тем, что окружность принимает вид эллипса в аксонометрии. Возникает вопрос: как рисовать эллипс? Чтобы построить окружность в аксонометрии используют следующие способы: - построение по вспомогательной квадратной сетке; - построение при помощи циркуля; По первому способу квадрат описывает окружность и делится на 4x4=16. Отмечаем точки пересечения линий сетки с линией окружности. Затем строим аксонометрическую проекцию сетки и на ней отмечаем точки A0, 10, 20, ..., 80. По этим точкам строим окружность, при помощи лекала. Данным способом окружность строится также в перспективе. 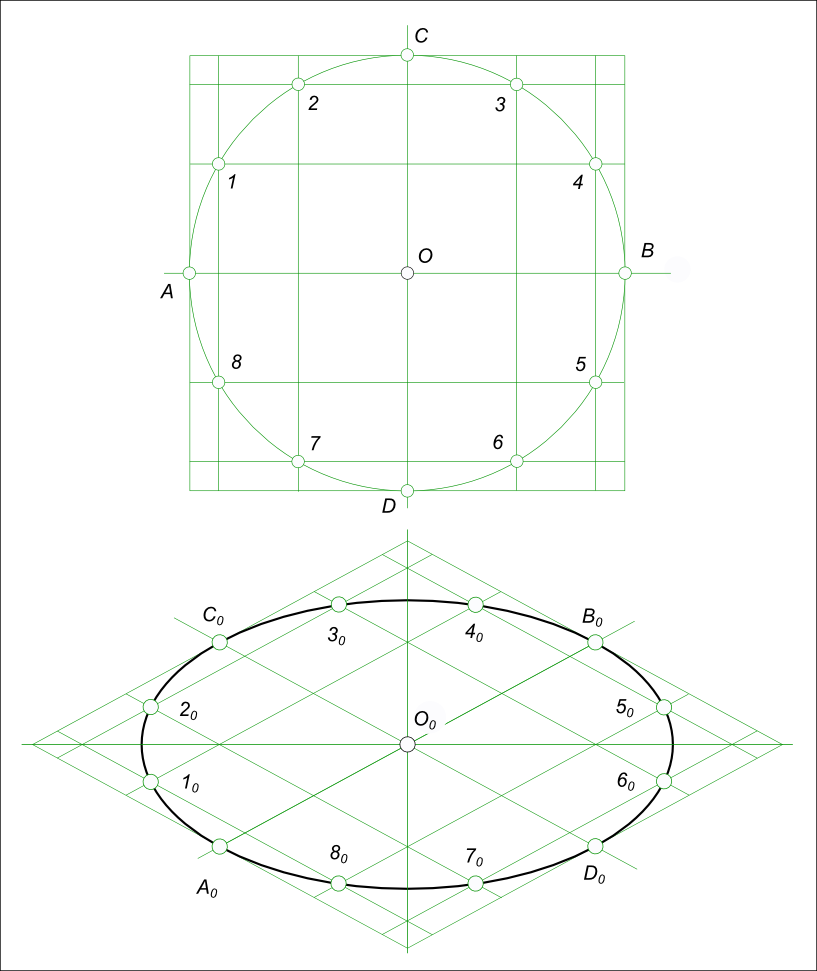 Построение аксонометрических проекций окружности Окружность для данного вида аксонометрической проекции - прямоугольной изометрии получилась получилась несколько больше своего действительного размера, в следствии применения приведенных коэффициентов искажения. По второму способу окружность строится при помощи циркуля Построение аксонометрических проекций окружности в косоугольной фронтальной диметрии 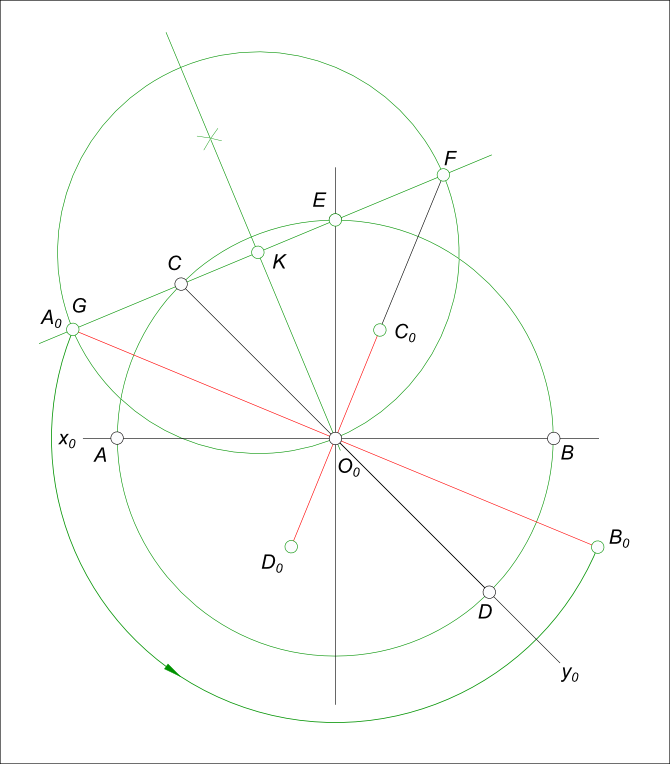 Построение аксонометрических проекций окружности Пусть окружность расположена параллельно горизонтальной плоскости проекции: - сначала определяем направление большой и малой оси эллипса, используя для этого построение показанное на рисунке Сопрягаемые диаметры AB и CD построены на аксонометрических осях x0 и y0, их центры совпадают с началом координат. Концы одного из диаметров (AB) соединим дугой окружности из центра O0. Восстановив перпендикуляр к диаметру в точке O0 отметим на их пересечении точку E. Соединяем точки C, E прямой линией. Находим середину отрезка CE - точку K. Из точки K описываем окружность радиусом KO0 и отмечаем точки F и G, в которых она пересекается с прямой CE. Длина половины большой оси равна отрезкам GE, CF, длина половины малой оси равна отрезкам CG, EF; - затем, после построения осей эллипса: 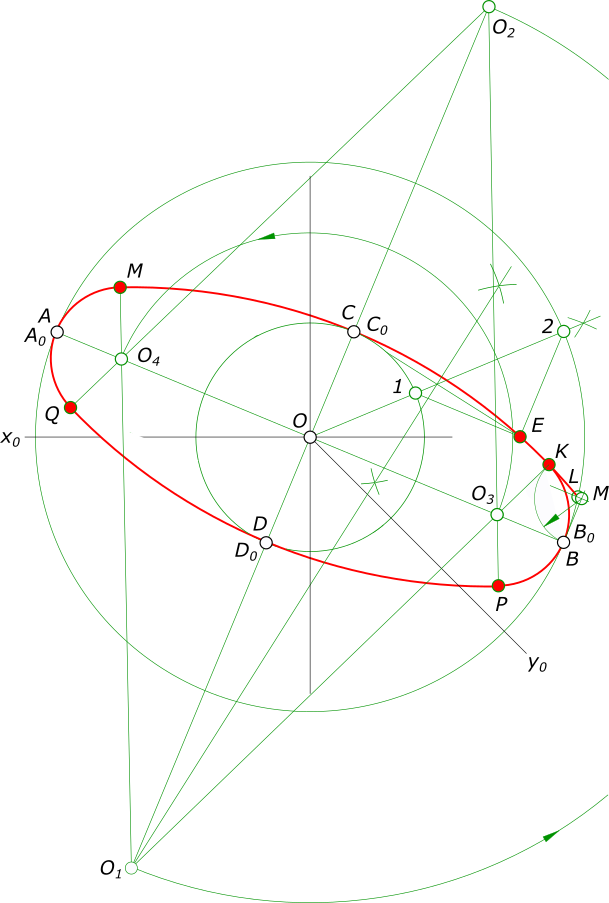 Построение аксонометрических проекций окружности - проводим прямую O - 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; - из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; - соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O1, которая определяет центр дуги CE; - строим точку O2 симметричную O1, относительно центра эллипса - O; - на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси - OB; - из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; - соединив прямой линией точки K и O1 на пересечении ее с большой осью находим точку O3, являющуюся центром дуги BK; - точку P находим на пересечении прямой O2O3 с дугой радиусом O3B. P - точка сопряжения дуг BK и BP; - точке O3 симметрична относительно центра эллипса точка O4; - аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения. Построение аксонометрических проекций окружности в прямоугольной изометрии 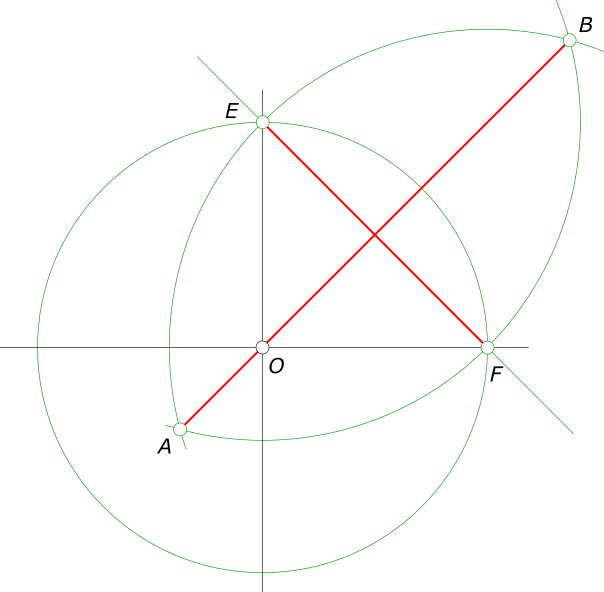 Построение аксонометрических проекций окружности Графически определяем размеры осей эллипса: - проводим две взаимно перпендикулярные линии; - приняв точку их пересечения за центр O, описываем из него окружность заданного диаметра и отмечаем точки E и F; - из точек E и F описываем дуги радиусом R = EF = FE и находим точки их пересечения A и B; - соединив точки A и B, получим большую ось эллипса, равную 1,22d; - соединив точки E и F, получим малую ось эллипса, равную 0,7d Пусть, строится окружность, расположенная параллельно горизонтальной плоскости проекции 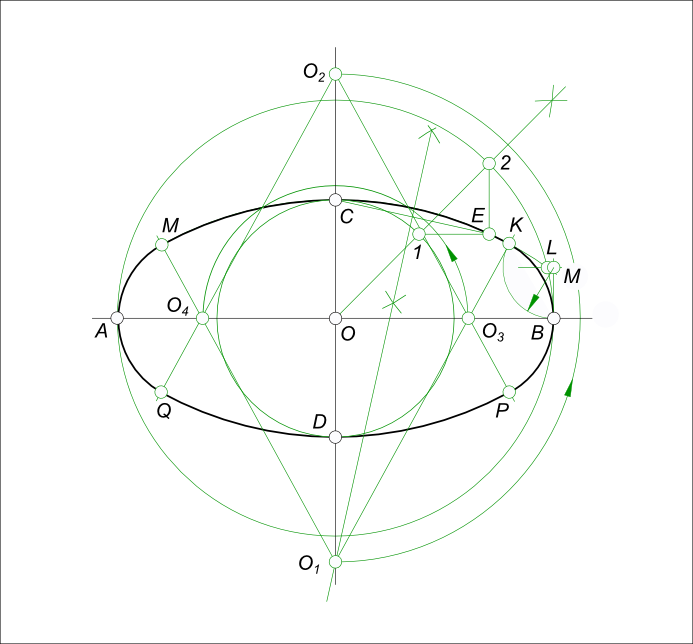 Построение аксонометрических проекций окружности где большая ось AB перпендикулярна свободной оси (z) и малая ось CD. - затем, после построения осей эллипса: - проводим прямую O - 2 делящую угол между осями пополам при этом находим точки 1 и 2 пересечения данной прямой с окружностями малой и большой оси; - из точки 1 проводим прямую параллельную большой оси, а из точки 2 проводим прямую параллельную малой оси и на их пересечении находим точку эллипса E; - соединяем точки E, C прямой линией. Через середину отрезка CE восстанавливаем к нему перпендикуляр до пересечения с малой осью в точке O1, которая определяет центр дуги CE; - строим точку O2 симметричную O1, относительно центра эллипса - O; - на пересечении дуг CE и 2B отмечаем точку L, проводим через данную точку прямую параллельную большой оси до пересечения ее в точке M с прямой BM, перпендикулярной большой оси - OB; - из центра M проводим дугу радиусом MB до пересечения ее с дугой CE в точке K, являющейся точкой сопряжения дуг овала; - соединив прямой линией точки K и O1 на пересечении ее с большой осью находим точку O3, являющуюся центром дуги BK; - точку P находим на пересечении прямой O2O3 с дугой радиусом O3B. P - точка сопряжения дуг QP и BP; - точке O3 симметрична относительно центра эллипса точка O4; - аналогично, построив точки сопряжения для левой половины , проводим дуги овала, предварительно удалив ненужные построения. Более просто выглядит построение окружности, расположенной параллельно горизонтальной плоскости проекции 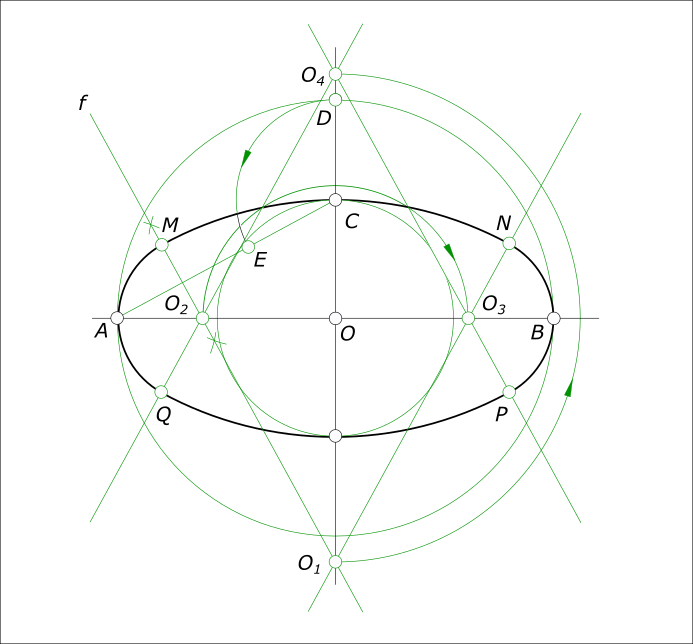 Построение аксонометрических проекций окружности +
|
