Графическая работа 12

    Графическая работа 12 раскрывает тему построения действительной величины сечения пирамиды SABCDE плоскостью α(α_H, α_V),
    которое выполнено ранее и развертки поверхности пирамиды.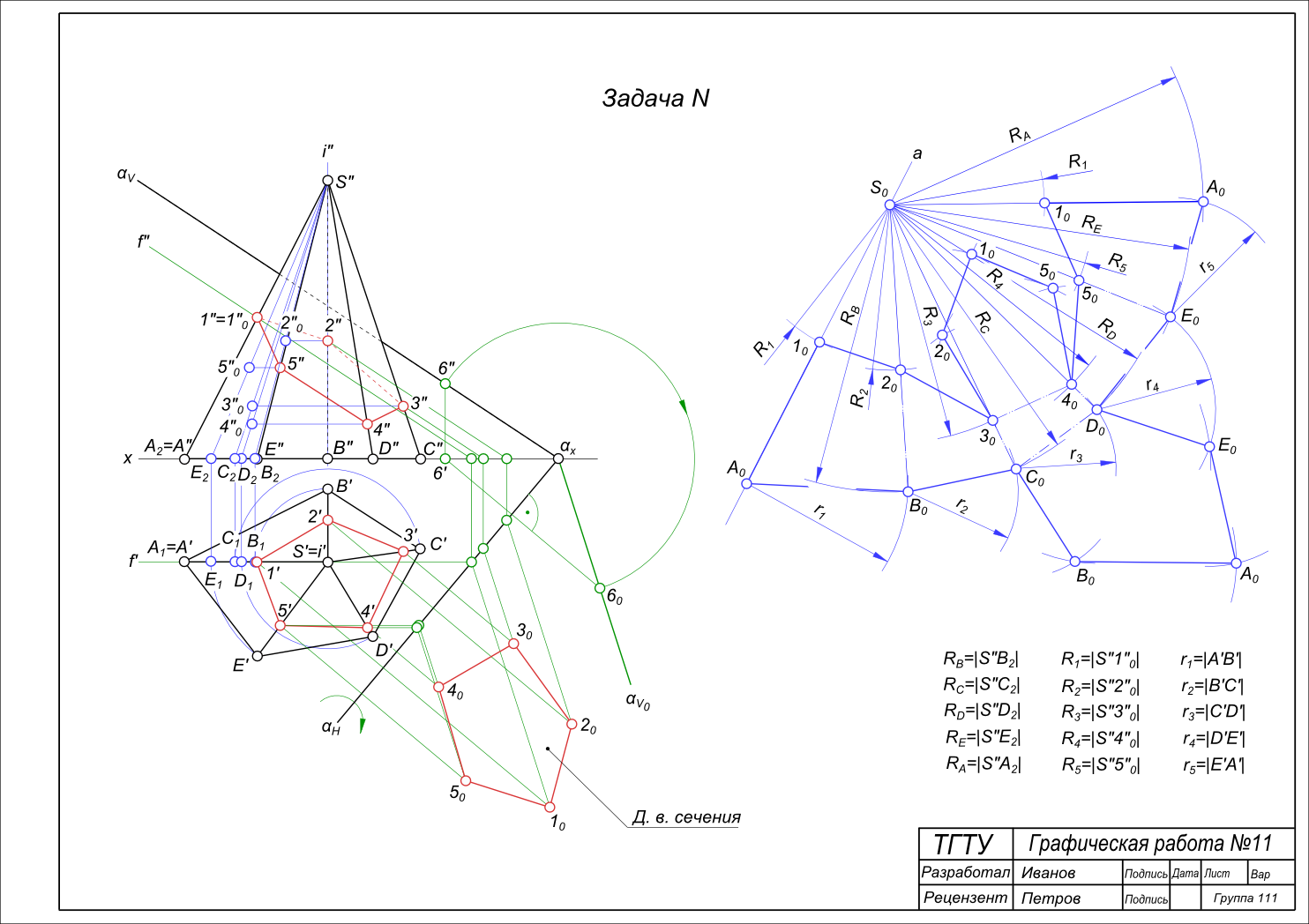

Графическая работа 12

                          Развертка боковой поверхности пирамиды будет представлять собой плоскую фигуру, состоящую из треугольников, являющихся гранями пирамиды.
                          Развертка усеченной пирамиды строится в два этапа.
                          Этап первый - построение действительной величины сечения.
                          Выполняется способом вращения вокруг следа плоскости α_H:
                          - взяв на следе плоскости α_V произвольную точку 6(6", 6`), строим ее совмещенное положение с плоскостью H - 6₀;
                          - строим совмещенное положение с плоскостью H фронтального следа плоскости α_V - α_V0 по точкам α_x и 6₀;
                          - строим совмещенное положение с плоскостью H точки сечения 1 - 1₀ находим на пересечении соответствующей фронтали плоскости α с проекцией линии вращения;
                          - аналогично строим совмещенное положение с плоскостью H остальных точек сечения 2, 3, 4, 5 - 2₀, 3₀, 4₀, 5₀.
                          Данные построения выделены зеленым цветом.

                          Развертка усеченной пирамиды - этап второй.
                          Построение выделено синим цветом.
                          Построение развертки выполняем способом треугольников:
                          - Определяем действительную величину ребер пирамиды способом вращения их вокруг оси i ∋ S также i ⊥ H,
                          в том же ключе строим действительную величину ребер усеченной пирамиды: A1, B2, C3, D4, E5;
                          - на прямой a произвольного положения откладываем величину |S₀A₀| ≅ |S"A₂|;
                          - из точки A₀ проводим дугу радиусом r₁ = |A`B`|;
                          - из точки S₀ проводим дугу радиусом R_B = |S"B₂|;
                          - пересечение дуг r₁ и R_B определяет положение вершины B₀ треугольника ΔS₀B₀A₀. ΔS₀B₀A₀ ≅ ΔSBA - грани пирамиды;
                          - из точки S₀ проводим дугу радиусом R₁ = |S"1"₀|, из точки S₀ проводим дугу радиусом R₂ = |S"2"₀|;
                          - пересечение дуги R₁ и S₀A₀ а также R₂ и S₀B₀ определяет положение вершин 1₀ и 2₀. 1₀2₀B₀A₀ ≅ 12BA - грани усеченной пирамиды;

                          Развертка усеченной пирамиды продолжается таким же образом и для остальных ее граней.
                          Графическая работа 12 завершается присоединением к построенной развертке боковой поверхности усеченной пирамиды основания A₀B₀C₀D₀E₀
                          и сечения 1₀2₀3₀4₀5₀, которые строятся способом триангуляции.

                         Построение сечения пирамиды смотри:  Сечение пирамиды плоскостью