Косоугольная диметрия

Косоугольная диметрия - (кабинетная проекция) картинная плоскость располагается параллельно фронтальной плоскости x0z, а направление проецирования выбирают так, что коэффициент искажения по оси 0y равен 0,5. Поэтому в косоугольной аксонометрии нет необходимости использовать приведенные коэффициенты искажения.

Косоугольная диметрия строится по следующему графическому алгоритму:
- Относим геометрическую фигуру к системе прямоугольных координат x, y и z, оси которой параллельны осям натуральной системы координат, и проходят через ее высоту (ось z) и ее основание (оси x, y);
- в принятой системе координат определяем координаты x, y и z точек геометрической фигуры на эпюре - с помощью измерительного циркуля и линейки.
- выполняем построение аксонометрического изображения точек.

Для построения аксонометрической проекции - Косоугольная диметрия - точки, например A, при заданном направлении аксонометрических осей необходимо отложить на них действительные координаты этой точки с учетом коэффициентов искажений:

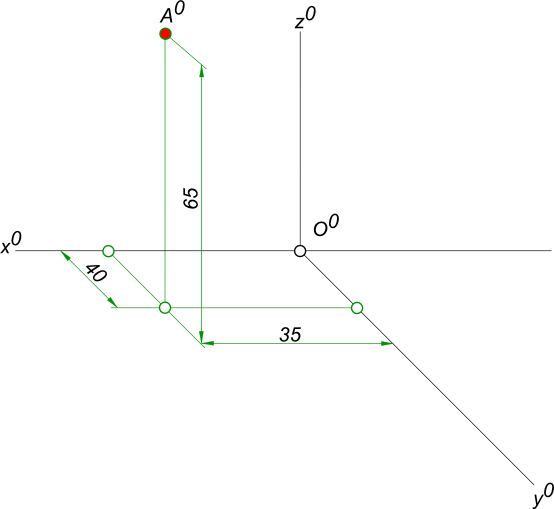Косоугольная диметрия

Построение аксонометрического изображения точки A, расположенной в пространстве.
Косоугольная диметрия строится по координатам точек (координаты точек определяем на эпюре по проекциям - с помощью измерительного циркуля и линейки). Например, точку A(35, 40, 65) строим следующим образом). Из начала координат О по оси x откладываем 30 мм, затем из полученной точки параллельно оси y откладываем 40 мм . Затем из полученной точки параллельно оси z откладываем 65 мм, и получаем точку A.

Рассмотрим построение аксонометрических изображений окружностей, расположенных в плоскостях проекций H, V и W. Если в плоскостях проекций H, V и W или параллельных им плоскостях располагается окружность диаметром d, то на картинную плоскость она спроецируется ортогонально в виде эллипса.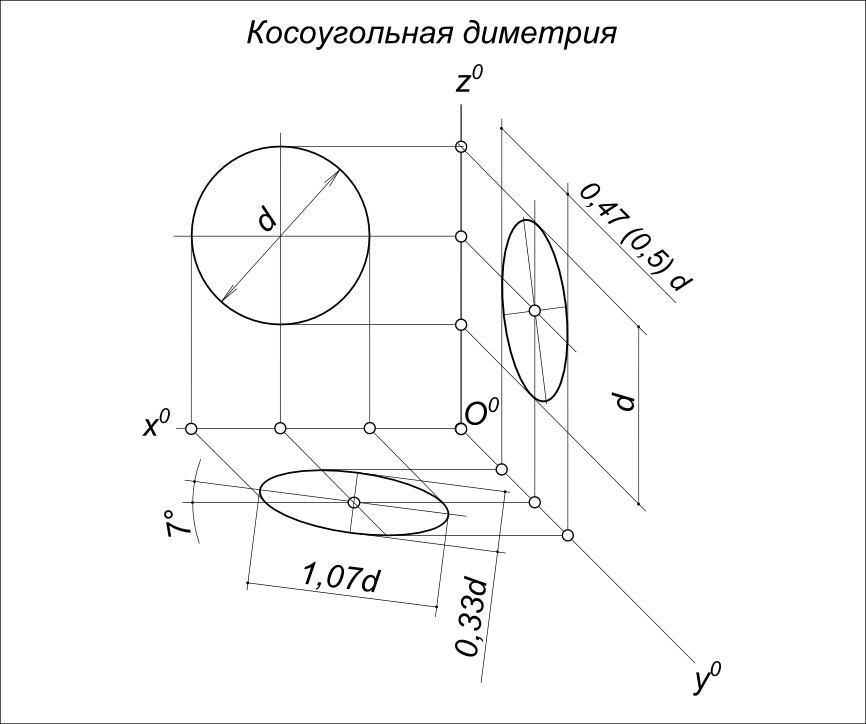

Косоугольная диметрия

Проекцией окружности, параллельной плоскостям проекций H и W, в косоугольная диметрии является эллипс, большая ось которого перпендикулярна «свободной» аксонометрической оси, а малая – совпадает с этой осью.
Построение аксонометрических проекций окружности смотри: Построение аксонометрических проекций окружности