Расстояние между скрещивающимися прямыми

Кратчайшее расстояние между скрещивающимися прямыми определяется величиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые. Эти плоскости называют плоскостями параллелизма.

Для того чтобы через скрещивающиеся прямые k и b провести взаимно параллельные плоскости α и β, достаточно через точку A (A ∈ k) провести прямую m, параллельную прямой b, а через точку B (B ∈ b) прямую n, параллельную прямой k.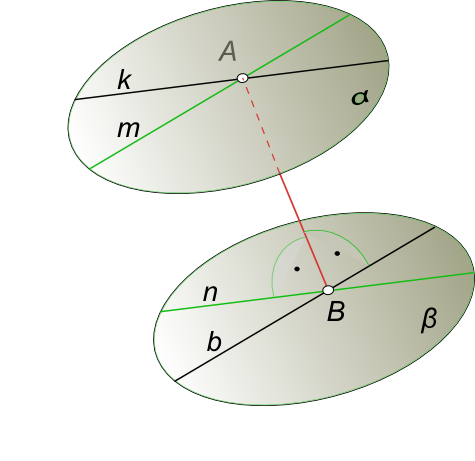

Расстояние между скрещивающимися прямыми

Пересекающиеся прямые k и m, b и n определяют взаимно параллельные плоскости α и β. Расстояние между плоскостями α и β равно искомому расстоянию между скрещивающимися прямыми k и b.

В качестве примера решаем задачу на кратчайшее расстояние между скрещивающимися прямыми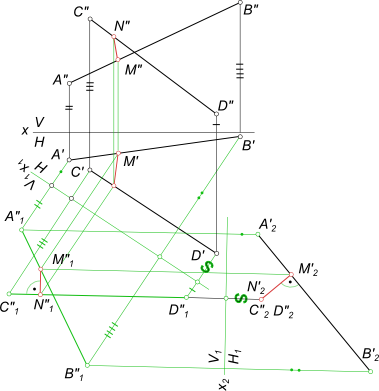

Расстояние между скрещивающимися прямыми

способом перемены плоскостей проекций. Здесь они заданны отрезками [AB] и [CD].
Кратчайшее расстояние между скрещивающимися прямыми способом прямоугольного треугольника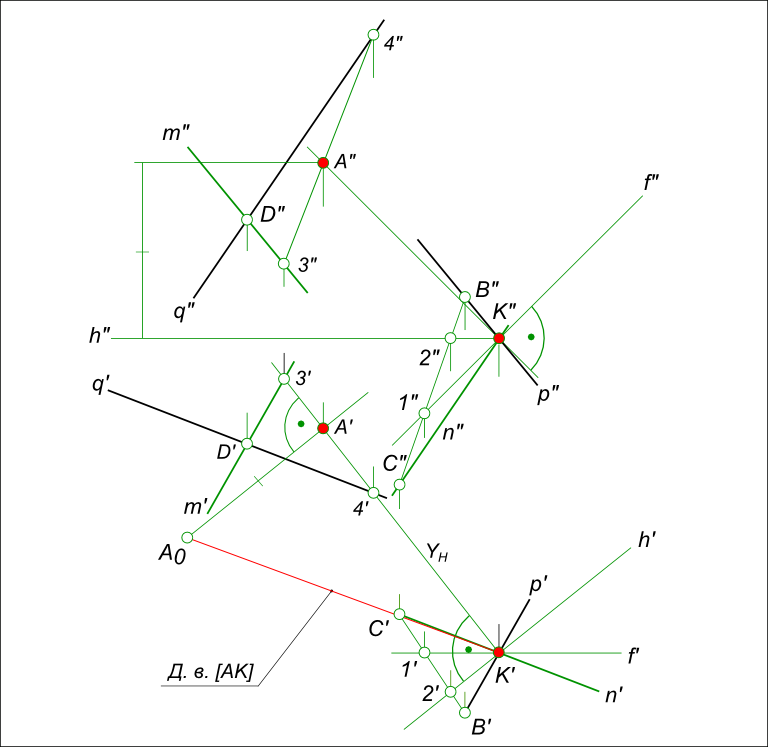

Расстояние между скрещивающимися прямыми

Здесь скрещивающиеся прямые q и p - через произвольно взятые точки D и K на скрещивающихся прямых q и p проводим прямые m║p и n║q. Таким образом, получаем две параллельные плоскости, каждая из пересекающихся прямых, параллельных друг другу;
- через точку K восстанавливаем перпендикуляр к плоскости из пересекающихся прямых p и n, для этого:
- построим точки C на прямой n и B на прямой p, соединив которые получим треугольный отсек плоскости CBK;
- проводим главные линии плоскости CBK горизонталь h и фронталь f; - находим точку пересечения перпендикуляра и плоскости пересекающихся прямых q и m:
- заключаем перпендикуляр в горизонтально проецирующую плоскость γ_H;
- строим линию пересечения 3 - 4 γ_H и плоскости пересекающихся прямых q и m;
- на пересечении линию пересечения 3 - 4 перпендикуляром находим точку A - точку встречи перпендикуляра опущенного из точки K на плоскость пересекающихся прямых q и m; - используя способ прямоугольного треугольника построим действительную величину перпендикуляра [KA] - кратчайшее расстояние между скрещивающимися прямыми q и p.

Решение задачи на определение угла между скрещивающимися прямыми смотри в статье: Угол между скрещивающимися прямыми.