Перспективное изображение прямой

Перспективное изображение прямой AB параллельной горизонтальной плоскости строится на основе системы проецирования перспективного изображения: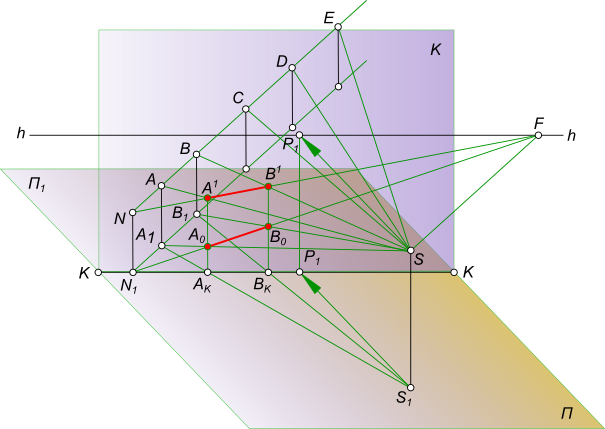

Перспективное изображение прямой

Перспективное изображение прямой имеет две характерные точки - начальную N и конечную F.
Начальная точка N представляет собой след прямой AB на картинной плоскости K.
Для того чтобы найти конечную точку F:
- выполняем построение изображения в перспективе промежуточных точек прямой C, D, E. - проводим лучи от наблюдателя S к каждой точке прямой. Луч, проведенный в точку, удаленную на бесконечно большое расстояние от картины, пройдет параллельно самой прямой и пересечет плоскость картины K в точке F, расположенной на линии горизонта hh, и получившей название точки схода.
Прямая NF - полная перспектива прямой AB, параллельной предметной плоскости П. Перспективное изображение прямой может быть получено в результате следующих построений:
- заключаем луч SA в горизонтально проецирующую плоскость α;
- находим линию пересечения двух плоскостей α и K;
- на линии пересечения находим A¹ в пересечении с лучом AS;
- найти точку A^K в и пересечении SA¹ луча с картинной плоскостью K;
- на линии пересечения находим A⁰ в пересечении с лучом A₁S;
- заключаем луч SB в горизонтально проецирующую плоскость α;
- находим линию пересечения двух плоскостей α и K;
- на линии пересечения находим B¹ в пересечении с лучом BS;
- найти точку B^K в пересечении SB¹ луча с картинной плоскостью K;
- на линии пересечения находим B⁰ в пересечении с лучом B₁S.
Точки A⁰ и B⁰ называются вторичной перспективной проекцией точек A и B.
Для того, чтобы перспективное изображение прямой было однозначно обратимым, необходимо перспективу прямой дополнить перспективой ее горизонтальной проекции, которая называется вторичной проекцией:
- N¹F - полная вторичная проекция прямой NF;
- A⁰B⁰ - вторичная проекция отрезка AB.

Для того, чтобы построить перспективное изображение прямой описанным способом необходимо: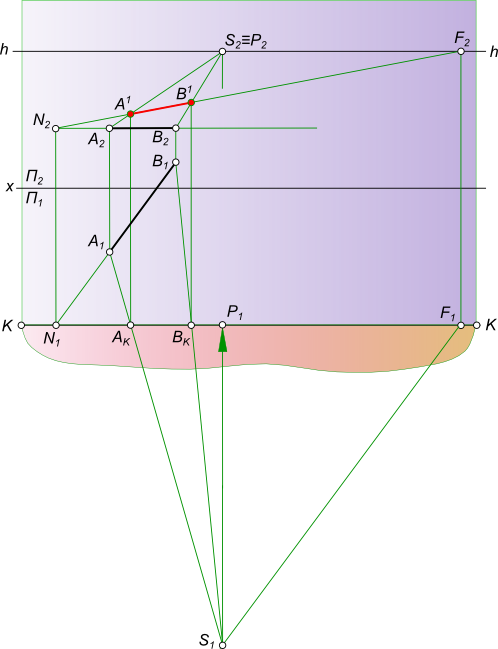

Перспективное изображение прямой

- задать объект AB двумя ортогональными проекциями A₁B₁ и A₂B₂, высоту линию горизонта hh и положение точки зрения S(S₁S₂);
- расположить на горизонтальной плоскости проекции П₁ картину при этом горизонтальная плоскость проекции служит также предметной плоскостью П(П=П₁), отмечая ее горизонтальный след KK между горизонтальной проекцией отрезка A₁B₁ и точкой стояния S₁ параллельным оси проекций Ox. В этом положении плоскость картины K будет параллельна фронтальной плоскости проекций П₂;
- задать высоту линию горизонта hh и положение точки зрения S(S₁S₂) на ортогональном чертеже;

Создав, таким образом, систему проецирования, строим перспективное изображение прямой:
- находим начальную точку N(N₁, N₂) как фронтальный след прямой AB;
- находим конечную точку или точку схода G(G₁, G₂), проведя луч SG(S₁G₁, S₂G₂) параллельно прямой AB до пересечения с картинной плоскостью;
- соединив прямой линией точки N₂ и G₂ получим полную перспективу прямой NF;
- находим перспективу A₁B₂ отрезка прямой AB, проводя проецирующие лучи SA(S₁A₁) и SB(S₁B₁) в пересечении их с плоскостью картины K.

Для того, чтобы перспективное изображение прямой A¹B¹ отрезка прямой AB было однозначно обратимым, необходимо перспективу прямой дополнить перспективой ее горизонтальной проекции A₁B₁, которая называется вторичной проекцией:
- N₁F - полная вторичная проекция прямой NF;
- A₀B₀ - вторичная проекция отрезка AB, построение которого ясно из чертежа.

Для того, чтобы перспективное изображение не накладывалось на фронтальную плоскость проекций и изображение, имеющееся на фронтальной плоскости П₂, не просвечивалось через картинную плоскость K,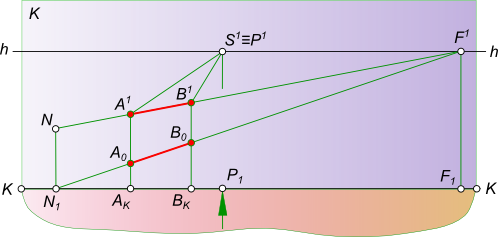

Перспективное изображение прямой

принято картину с изображениями принадлежащими ей, вычерчивать на свободном месте этого же листа или располагать на отдельном листе.

Ортогональными проекциями заданы прямые AB и CD, точка зрения S, плоскость картины и линия горизонта hh.
Перспективное изображение прямой перпендикулярной картинной и параллельной предметной плоскостям.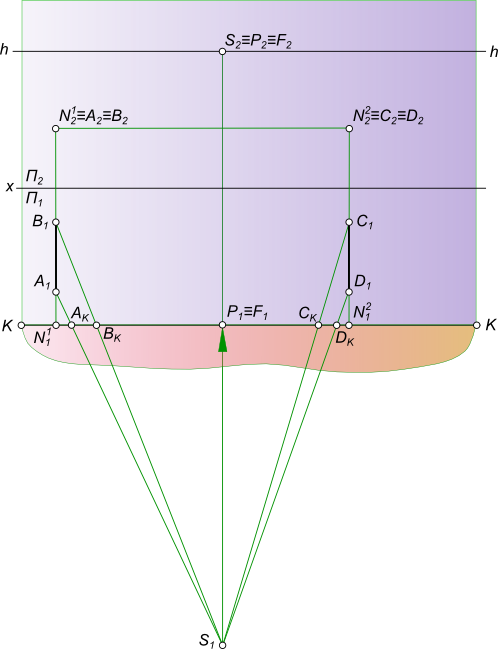

Перспективное изображение прямой

может быть выполнено описанным способом для этого необходимо:
- найти начальные точки N¹ N² на пересечении продолжения прямых AB и CD с картинной плоскостью K;
- найти конечные точки F¹ и F² прямых AB и CD, проводя лучи из точки зрения S параллельные заданным прямым AB и CD. F¹≡F² = F;
- провести лучи SA, SB, SC и SD, получая на следе картинной плоскости KK точки A_K,B_K и C_K,D_K;
- на свободное место чертежа перенести картину и все точки расположенные на ней, начиная с точек N¹ N² A_K,B_K и C_K,D_K, P, отмеченных на основании картины;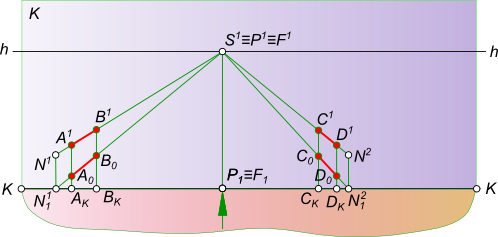

Перспективное изображение прямой

- отложить высоты точек N¹, N² и получить начальные точки на картинной плоскости;
- соединить начальные точки N¹ N² с точкой схода F¹, получая полные перспективные изображения прямых N¹F¹ и N²F¹;
- найти перспективы отрезков AB и CD - A¹B¹ и C¹D¹ соответственно;
- построить вторичные перспективы полных перспектив прямых N1P N2P;
- найти вторичные проекции отрезков AB и CD - A₀B₀ и C₀D₀ соответственно.

Перспективное изображение прямой перпендикулярной предметной и параллельной картинной плоскостям.
Ортогональными проекциями заданы прямые AB и CD, точка зрения S, плоскость картины и линия горизонта hh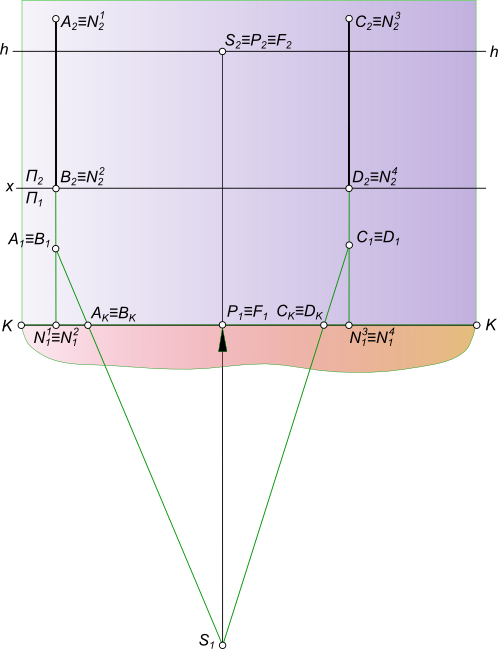

Перспективное изображение прямой

На перспективном изображении у таких прямых не будет начальных точек N(AB) и N(CD). Не будет у таких прямых и точек схода F, так как лучи, проведенные из точки зрения, параллельно прямым, будут параллельны также картине и не пересекут ее.
Перспективное изображение прямой, занимающей положение вертикальной линии строят с помощью дополнительных прямых, перспективы которых имеют начальные и конечные точки. Проведем через концы отрезков AB и CD прямые перпендикулярные картине.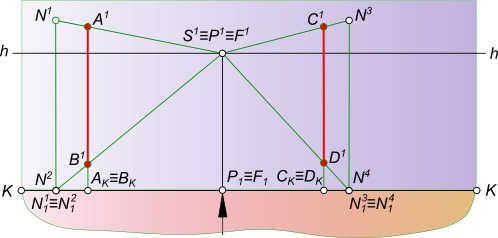

Перспективное изображение прямой

И построим перспективу этих дополнительных линий, а на них найдем перспективные изображения A¹B¹ и C¹D¹ вертикальных отрезков AB и CD.

Ортогональными проекциями заданы прямые AB и CD, точка зрения S, плоскость картины и линия горизонта hh.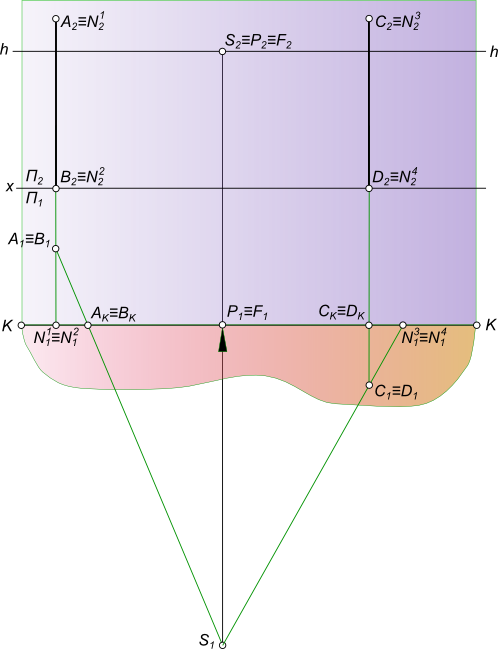

Перспективное изображение прямой

Перспективное изображение прямой перпендикулярной предметной и параллельной картинной плоскостям. В случае, когда одна из прямых AB находится в предметном пространстве, а другая CD - в промежуточном пространстве.
На перспективном изображении у таких прямых не будет начальных точек N(AB) и N(CD). Не будет у таких прямых и точек схода F, так как лучи, проведенные из точки зрения, параллельно прямым, будут параллельны также картине и не пересекут ее.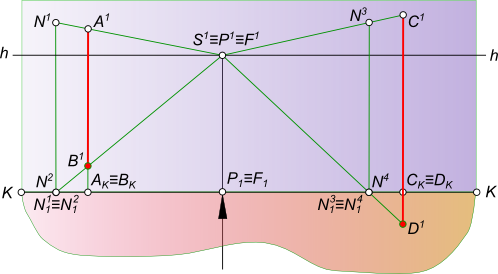

Перспективное изображение прямой

Перспективное изображение прямой, занимающей положение вертикальной линии строят с помощью дополнительных прямых, перспективы которых имеют начальные и конечные точки. Проведем через концы отрезков AB и CD прямые перпендикулярные картине и построим перспективу этих дополнительных линий, а на них найдем перспективные изображения A¹B¹ и C¹D¹ вертикальных отрезков AB и CD.

Ортогональными проекциями заданы прямая AB, точка зрения S, плоскость картины и линия горизонта hh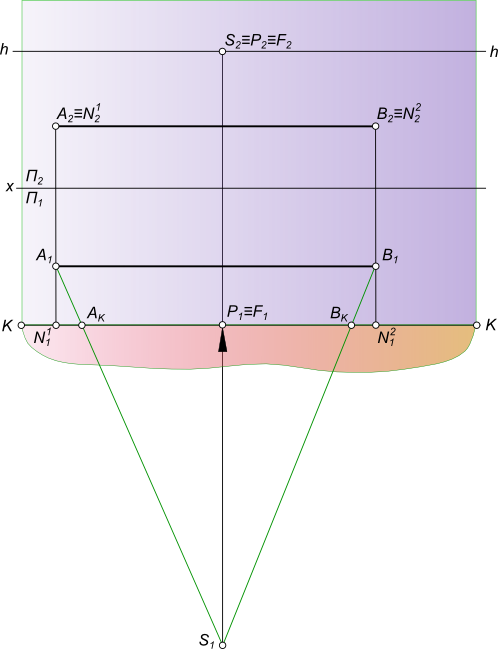

Перспективное изображение прямой

Перспективное изображение прямой параллельной предметной и картинной плоскостям. На перспективном изображении у такой прямой не будет начальной точки N. Не будет у такой прямой и точки схода F, так как лучи, проведенные из точки зрения, параллельно прямой, будут параллельны также картине и не пересекут ее.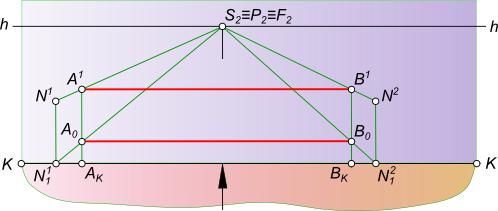

Перспективное изображение прямой

Перспективное изображение прямой, занимающей данное строят с помощью дополнительных прямых, перспективы которых имеют начальные и конечные точки. Проведем через концы отрезка AB прямые перпендикулярные картине и построим перспективу этих дополнительных линий, а на них найдем перспективные изображения A¹B¹ отрезка AB и его вторичную проекцию A₀B₀.

Перспективное изображение прямой общего положения может быть выполнено с помощью вспомогательных горизонтальных прямых, проведенных через концы заданного отрезка прямой или построением полной перспективы прямой. Выбор способа построения происходит в зависимости от расположения прямой в пространстве:
- Перспективное изображение прямой общего положения, параллельного картинной плоскости.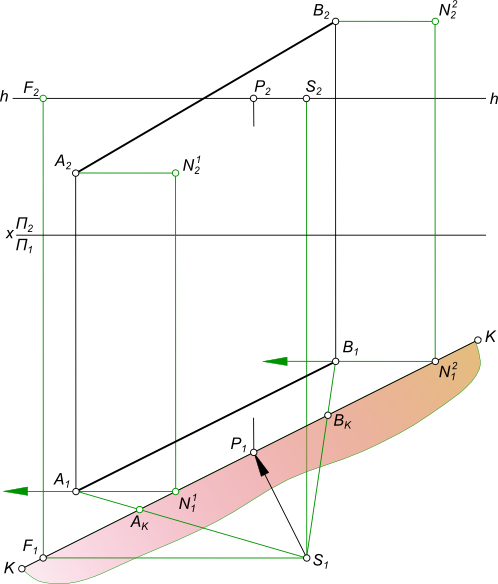

Перспективное изображение прямой

В данном случае, при построении перспективы отрезка прямой нельзя получить начальную и конечную точки прямой для построения перспективных проекций, так как AB║K и центрально-проецирующий луч, проведенный из точки зрения S параллельно AB, не пересечет плоскость картины;
Рисунок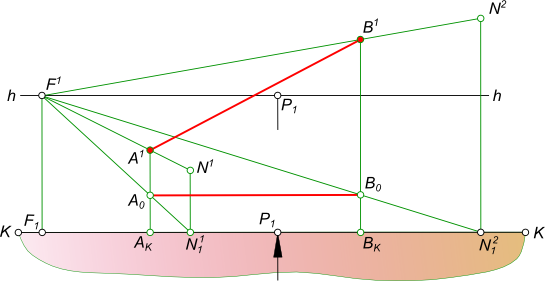

Перспективное изображение прямой

Картину с изображениями принадлежащими ей, вычерчиваем на свободном месте этого же листа или располагаем на отдельном листе. Строим полную перспективу вспомогательных прямых, на которые переносим точки A_K и B_K, получая точки A¹ и B¹, A₀ и B₀. Соединив между собой одноименные точки получим перспективное изображение прямой A¹B¹ и вторичную проекцию прямой A₀B₀.

- Перспективное изображение прямой общего положения, не параллельного картинной плоскости.
Ортогональными проекциями заданы прямая AB, точка зрения S, плоскость картины и линия горизонта hh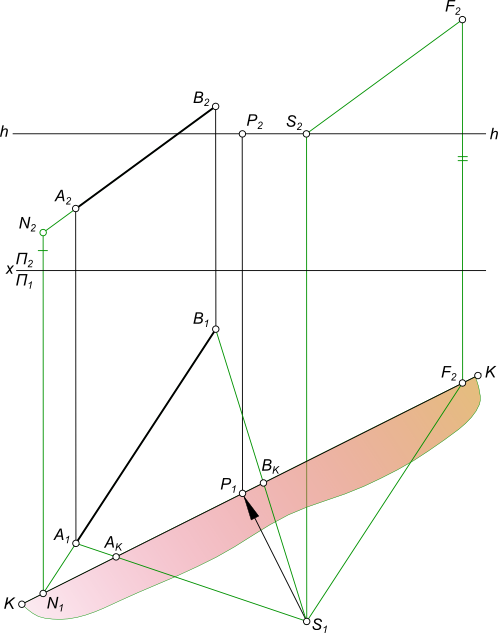

Перспективное изображение прямой

В данном случае, взаимное положение отрезка и картины позволяет при построении перспективы отрезка прямой получить начальную и конечную точки прямой для построения перспективных проекций, так как центрально-проецирующий луч, проведенный из точки зрения S параллельно AB, пересечет плоскость картины в конечной точке - точке схода F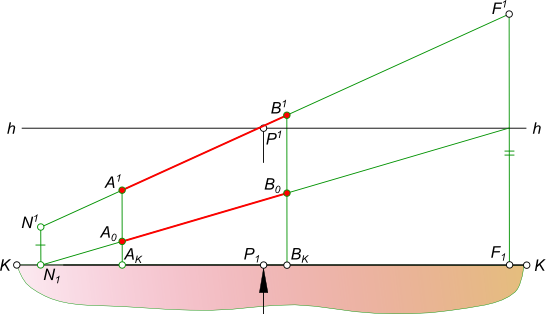

Перспективное изображение прямой

Картину с изображениями принадлежащими ей, вычерчиваем на свободном месте этого же листа или располагаем на отдельном листе. Строим полную перспективу прямой, на которую переносим точки A_K и B_K, получая точки A¹ и B¹, A₀ и B₀. Соединив между собой одноименные точки получим перспективное изображение прямой A¹B¹ и вторичную проекцию прямой A₀B₀.