Угловая перспектива

Угловая перспектива применяется при изображении отдельных объектов, в этом случае картинная плоскость располагается под углом к объекту.
Перспектива плоскости треугольника ABC может быть построена если заданы ее ортогональные проекции.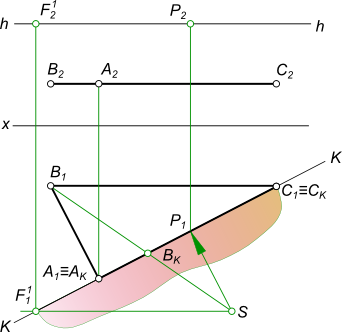

Угловая перспектива

Угловая перспектива плоскости треугольникаABC может быть построена, если будет обеспечено последовательное выполнение следующих действий: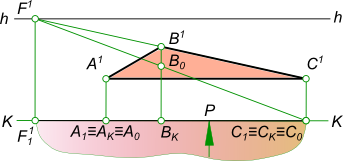

Угловая перспектива

- выбор положения следа картинной плоскости. Плоскость картины совпадает с стороной AC;
- выбор положения точки зрения S выполняем так, чтобы главный луч зрения SP, перпендикулярный картинной плоскости, проходя через нее, делил перспективное изображение плоскости треугольника примерно пополам;
- в дополнение к точкам A_KC_K строим точку B_K, проводя луч SB₁;
- строим перспективное изображение A¹C¹ стороны AC;
- параллельно B₁C₁ проводим вспомогательный луч из точки S и находим точку схода стороны BC;
- точку схода стороны BC переносим на с основания картинной плоскости на заданную линию горизонта в точку F¹;
- из точки F¹ проводим прямые F¹C¹ и F¹C₀;
- в пересечении перпендикуляра к основанию картины в точке B^K с прямыми F¹C¹ и F¹C₀ находим точки B¹ и B⁰;
- соединяем прямой линией точки A¹B¹, замыкая контур треугольника. Таким образом, получена Угловая перспектива плоскости треугольника ABC.

Угловая перспектива плоскости окружности может быть построена если заданы ее ортогональные проекции.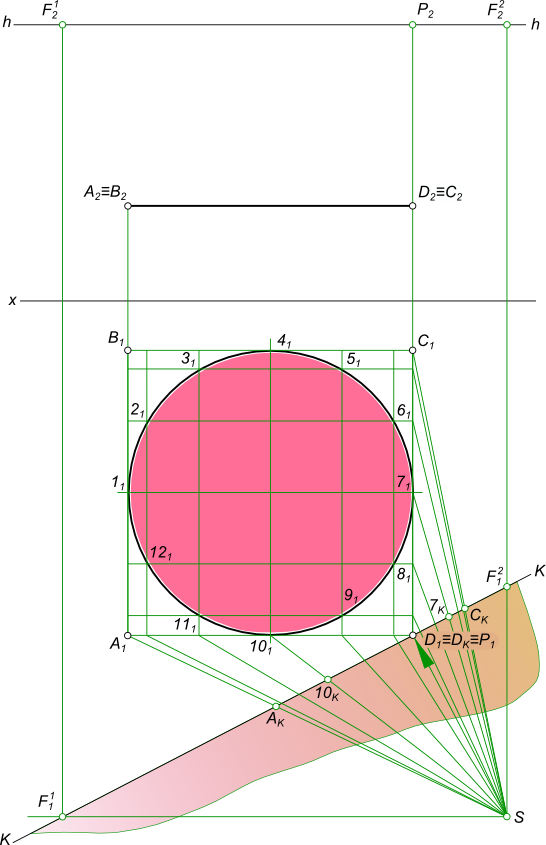

Угловая перспектива

Угловая перспектива плоскости окружностим ожет быть построена, если будет обеспечено последовательное выполнение следующих действий: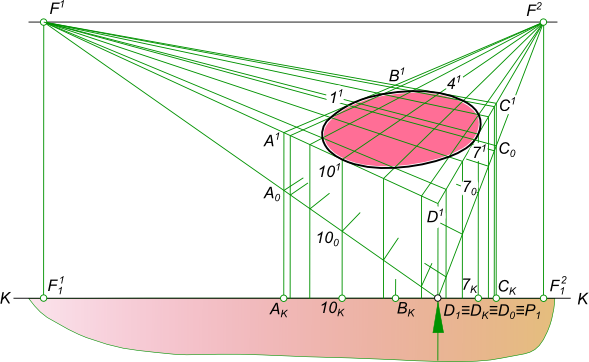

Угловая перспектива

- описываем вокруг окружности квадрат ABCD ;
- делим дугу окружности на 12 равных частей;
- строим, через эти 12 точек на дуге окружности, сетку в квадрате;
- выполняем построение перспективного изображения плоскости квадрата ABCD и сетки;
- выбор положения следа картинной плоскости. Плоскость картины совпадает с одной из вершин квадрата или с одной из его сторон;
- выбор положения точки зрения S выполняем так, чтобы главный луч зрения SP, перпендикулярный картинной плоскости, проходя через нее, делил перспективное изображение квадрата примерно пополам;
- в дополнение к имеющейся точке D1 строим точки A1 и C1, проводя к ним лучи SA1 и SC1 и отмечая точки AK и CK в пересечении лучей с картинной плоскостью;
- строим перспективное изображение A¹C¹ стороны AC;
- параллельно A₁D₁ проводим вспомогательный луч из точки S и находим точку схода стороны AD;
- параллельно D₁C₁ проводим вспомогательный луч из точки S и находим точку схода стороны DC;
- точку схода стороны AD переносим на с основания картинной плоскости на заданную линию горизонта в точку F¹;
- точку схода стороны DC переносим на с основания картинной плоскости на заданную линию горизонта в точку F²;
- из точки F¹ проводим прямые F¹D¹ и F¹D₀;
- в пересечении перпендикуляра к основанию картины в точке A^K с прямыми F¹D¹ и F¹D₀ находим точки A¹ и D⁰;
- из точки F² проводим прямые F²D¹ и F²D₀;
- в пересечении перпендикуляра к основанию картины в точке C^K с прямыми F²D¹ и F²D₀ находим точки C¹ и C⁰;
- из точки F¹ проводим прямые F¹C¹, из точки F² проводим прямые F²A¹ и в их пересечении находим B¹;
- соединяем прямыми линиями точки A¹, B¹, C¹ и D¹, получая замкнутый контур перспективного изображения плоскости квдрата;
- соединяем плавной линией точки на перспективном изображении сетки, получая замкнутый контур перспективного изображения плоскости окружности. Угловая перспектива плоскости окружности занимающей какие-либо другие положения в пространстве строится по тому же принципу.

Угловая перспектива отдельного здания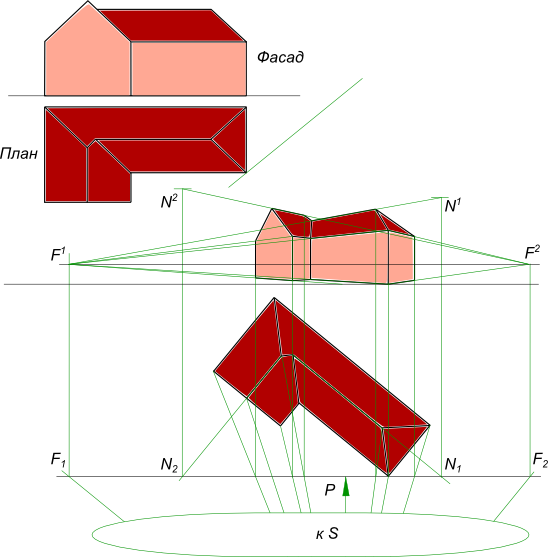

Угловая перспектива