Вспомогательные цилиндрические и конические поверхности

Вспомогательные цилиндрические и конические поверхности могут быть использованы в ряде случаев, с их помощью находят пересечение поверхностей вращения. Когда определяют линию пересечения двух поверхностей, из которых одна линейчатая (цилиндрическая или коническая), а другая произвольная поверхность вращения, целесообразно в качестве посредников использовать цилиндрические или конические поверхности.

Найти линию пересечения эллиптического цилиндра α и кольца β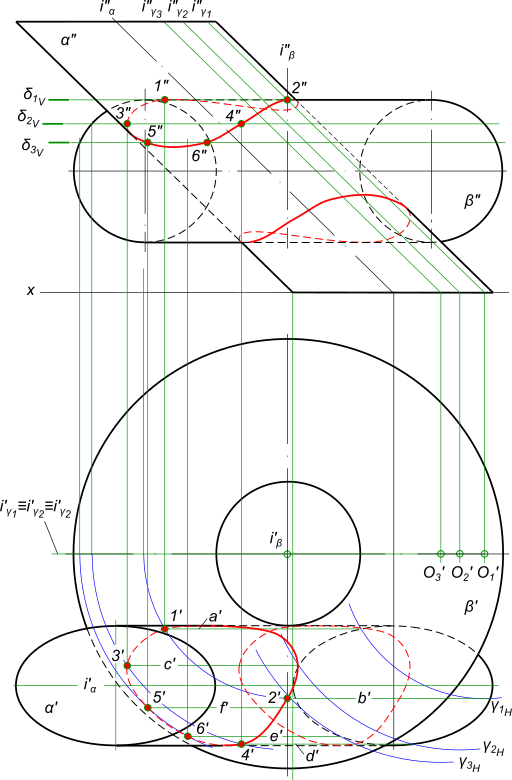

Вспомогательные цилиндрические и конические поверхности

Здесь в качестве вспомогательных секущих поверхностей целесообразно использовать поверхности эллиптических цилиндров, оси которых параллельны оси заданной цилиндрической поверхности α. За направляющие цилиндрических поверхностей следует принять окружности - параллели кольцевой поверхности β. Точки линии пересечения эллиптического цилиндра α и кольца β находим следующим путем:
- определяем границы области, в которой следует проводить вспомогательные секущие плоскости, определим высшие точки линии пересечения - их две 1 и 2 и низшие точки линии пересечения - их также две. - пересекаем поверхность кольца плоскостями δ1, δ2, δ3, ..., параллельными плоскости H;
- полученные в сечении окружности принимаем за направляющие цилиндрических поверхностей H;
- строим горизонтальные следы цилиндрических поверхностей γ1H, γ2H, γ3H, ... и отмечаем точки пересечения этих следов с аH;
- через полученные точки проводим прямолинейные образующие a, b, c, d, e и f по которым поверхности γ1, γ2, γ3, ... пересекают заданную поверхность α;
- строим горизонтальные проекции линий пересечения поверхности кольца плоскостями δ1, δ2, δ3, ... т. е. окружности;
- отмечаем точки 1, 2, 3, 4, 5 и 6 пересечения этих окружностей с соответствующими прямолинейными образующими цилиндрической поверхности α.
Проведя необходимое количество вспомогательных цилиндрических поверхностей можно с их помощью определить достаточное число точек необходимых для построения линии пересечения поверхностей α и β.

Найти линию пересечения поверхности вращения α с произвольной конической поверхностью β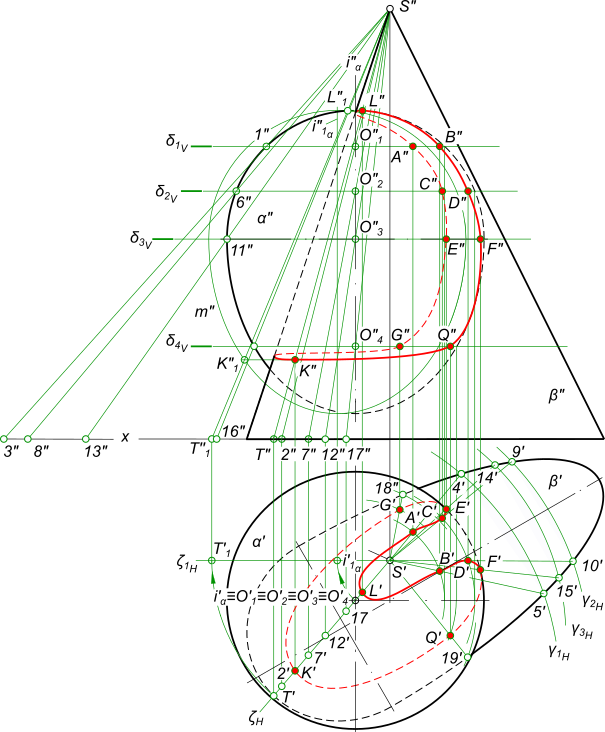

Вспомогательные цилиндрические и конические поверхности

Заданы поверхность вращения α и произвольная коническая поверхность β. Для определения линии пересечения заданных поверхностей воспользуемся вспомогательными коническими поверхностями γ1, γ2, γ3, γ4 вершины которых совпадают с вершиной заданной конической поверхности β, а направляющими этих поверхностей являются окружности проведенные на поверхности вращения.
Построение линии пересечения поверхности вращения α с произвольной конической поверхностью β выполняем в следующей последовательности:
- Чтобы определить границы области, в которой следует проводить вспомогательные секущие плоскости, определим высшую L и низшую K точки линии пересечения. Для этого вводим вспомогательную горизонтально-проецирующую плоскость ζ, проходящую через ось i поверхности вращения α и вершину S конической поверхности. Плоскость ζ пересечет коническую поверхность по образующей ST, а поверхность вращения - по меридиану m. Для определения точек пересечения меридиана с образующей повернем плоскость ζ, которой они принадлежат, вокруг оси перпендикулярной плоскости H и проходящей через вершину конуса S, до положения параллельного плоскости V. Находим фронтальные проекции точек L"1 и K"1, а затем L" и K". Зная проекции L" и K", определяем горизонтальные проекции L` и K`. Точки L и K указывают границы области для проведения вспомогательных секущих плоскостей δ1, δ2, δ3, δ4;
- на поверхности вращения проводим ряд окружностей, которые рассматриваем как результат пересечения поверхности α семейством плоскостей {δ}, параллельных плоскости H;
- принимаем эти окружности за направляющие конических поверхностей γ1, γ2, γ3, γ4 ... с вершиной в точке S. Горизонтальные следы этих поверхностей γ1H, γ2H, γ3H, γ4H есть окружности проведенные из центров 2, 7, 12, 17. Радиусами соответственно равными фронтальным проекциям отрезков /2", 3"/, /7", 8"/, /12", 13"/, /16", 17"/;
- определяем прямые (S`4`), (S`5`), (S`9`), (S`10`), (S`14`), (S`15`), (S`18`), (S`19`) по которым вспомогательные секущие поверхности γ1, γ2, γ3, γ4 пересекают заданную коническую поверхность β;
- отмечаем точки пересечения этих прямых с соответствующими окружностями. Точки A, B, C, D, E, F, G, Q принадлежат искомой линии пересечения;
- соединив одноименные проекции полученных точек плавной кривой, получим линию пересечения заданных поверхностей.