Пересечение прямой с плоскостью

Пересечение прямой с плоскостью происходит в некоторой точке, когда прямая не принадлежит плоскости и не параллельна ей.
Точку встречи прямой с плоскостью находят с помощью вспомогательной плоскости частного, а в некоторых случаях, общего положения:
- прямая заключается в вспомогательную плоскость;
- находится линия пересечения плоскостей;
- находится точка встречи в пересечении прямой с линией пересечения плоскостей заданной и вспомогательной.
Вспомогательную плоскость, в проекциях с числовыми отметками, задают двумя горизонталями, проведенными через концы отрезка прямой так, чтобы они пересекались с горизонталями плоскости тех же уровней и в пределах чертежа.
Нахождение точки встречи K прямой A15B10 с плоскостью α, заданной масштабом уклона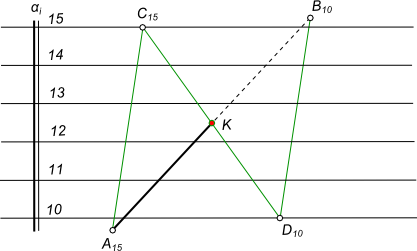

Пересечение прямой с плоскостью

выполняем согласно приведенному выше алгоритму.
Если при решении задачи вспомогательная плоскость задается горизонталями, то такой способ решения называют способом горизонталей.
Также задача на пересечение прямой с плоскостью может быть решена способом профилей, сущность которого состоит в том что вспомогательная плоскость занимает горизонтально проецирующее положение, которое затем совмещают с плоскостью проекций.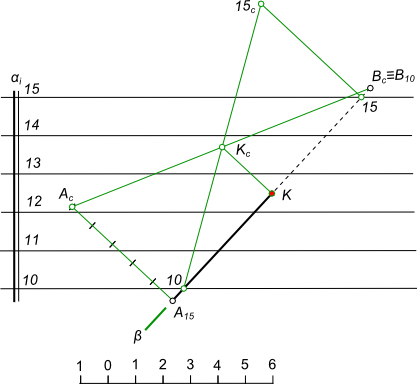

Пересечение прямой с плоскостью

Положение точки K найдено поднятием вспомогательной плоскости β из совмещенного положения в первоначальное.