Прямая в плоскости

Прямая в плоскости в проекциях с числовыми отметками - это может быть горизонталь заданной плоскости.
Горизонталью называется прямая, лежащая в плоскости параллельно горизонтальной плоскости проекций.
Пусть, плоскость задана проекциями трех точек A5, B8 и C2

Прямая в плоскости

Требуется провести горизонтали заданной плоскости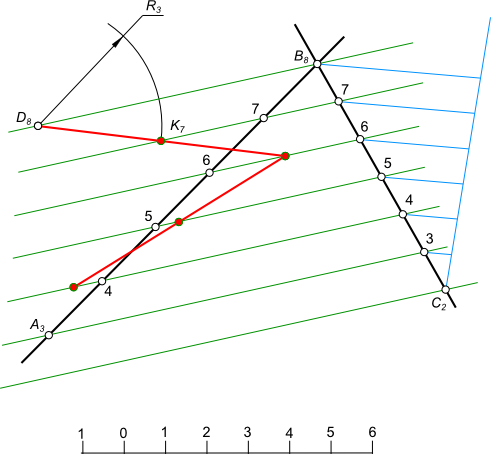

Прямая в плоскости

Прямая в плоскости - горизонталь заданной плоскости строится следующим образом:
- соединяем прямыми линиями проекции точек A5 и B8, проекции точек B8 и C2;
- градуируем прямую с наибольшей разностью отметок B8C2;
- соединяем прямыми линиями точки имеющие одинаковые отметки точку A5 с точкой на линии B8C2 имеющей отметку 5 и получаем направление горизонталей;
- проводим прямые, через остальные отметки проградуированной прямой B8C2, в направлении горизонталей и получаем искомые горизонтали заданной плоскости.
Прямая в плоскости в проекциях с числовыми отметками - это может быть прямая с заданным уклоном.
Пусть, плоскость задана проекциями трех точек A5, B8 и C2.
Требуется в плоскости из точки D8 провести прямую с заданным уклоном i=1/3.
Прямая в плоскости A5B8C2 с заданным уклоном i=1/3 строится следующим образом:
- получаем искомые горизонтали заданной плоскости;
- определяем интервал l=1/i=1/(1/3)=3;
- из точки D8 радиусом равным 3 единицам засекаем горизонталь 7. Получая в месте пересечения точку K7, определяющей искомое положение отрезка D8K7 с заданным уклоном i=1/3.