Проекции прямоугольного треугольника

Построить Проекции прямоугольного треугольника ABC, если его катет AB(A`B`, ...) принадежит горизонтальной прямой h(h`, h"), катеты равны между собой, а вершина C принадлежит прямой m(m`, ...) и zC больше zB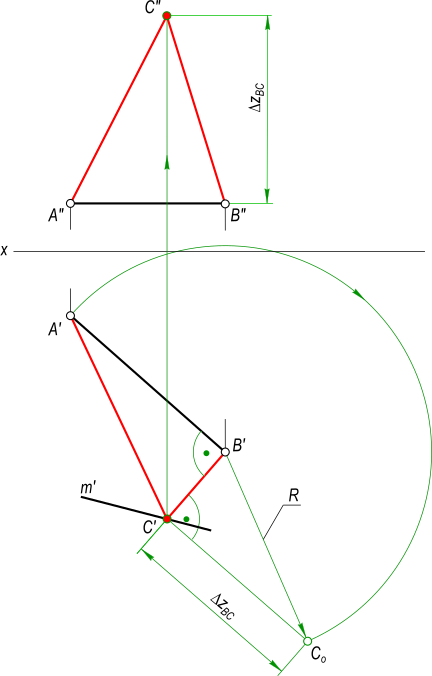

Проекции прямоугольного треугольника

AB - один из катетов прямоугольного треугольника, представляет собой прямую уровня - горизонтальную прямую так как A"B" || Ox. На горизонтальную плоскость проекции он проецируется в натуральную величину.
Выполняем построение BC:
- прямой угол при вершине B проецируется без искажения на горизонтальную плоскость проекции, следовательно здесь можно провести направление для катета BC;
- в пересечении направления катета BC с m` получим C`.
По способу прямоугольного треугольника определяем Δz = zC-zB:
- из центра O описываем дугу радиусом R=|AB|=A`B` до пересечения с направлением перпендикуляра в точке C0;
- определяем разницу аппликат катета BC - Δz.
Откладываем Δz на фронтальной плоскости проекций от точки B" и по линии проекционной связи находим точку C".

Построить проекции прямоугольного равнобедренного треугольника ABC, катет которого BC лежит на прямой MN. A(60,40,10), M(75,10,30); N(15,25,30).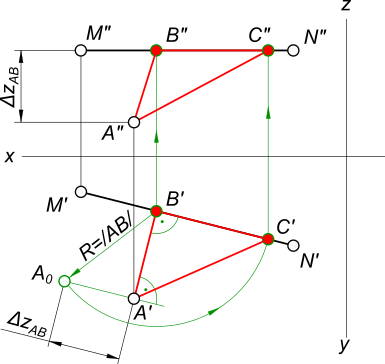

Проекции прямоугольного треугольника

Так как zM=zN делаем вывод, что отрезок MN - горизонтальная прямая и мы можем опустить из точки A перпендикуляр на него. В пересечении которого с M`N` находим B` и затем по линии проекционной связи B".
Находим натуральную величину катета AB способом прямоугольного треугольника:
- через точку A проводим перпендикуляр к AB и на нем откладываем ΔzAB и находим A0 и BA0;
- откладываем на отрезке MN катет BC, описывая дугу радиуса R=/AB/ и отмечая точку C` и по линии проекционной связи C";
- вершины A`B`C` и A"B"C" соединяем прямыми линиями, получая проекции искомого треугольника.

Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).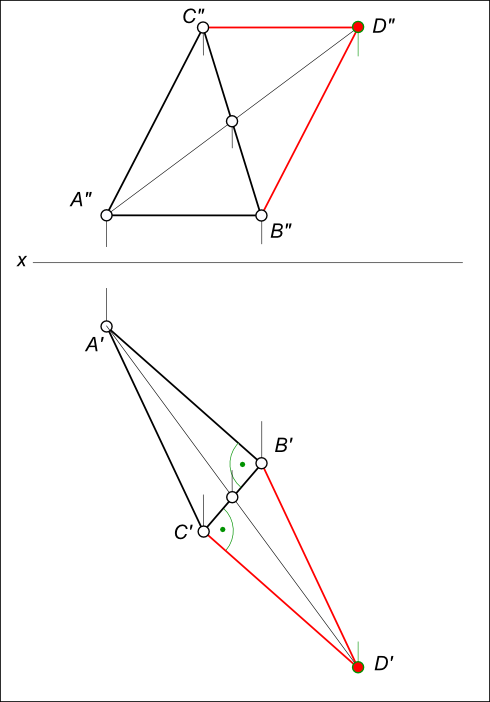
Построить фронтальную и горизонтальную проекции параллелограмма ABCD

Проекции прямоугольного треугольника

Построение параллелограмма заключается:
- в проведении BD // AC; - в проведении CD // AB.

Даны проекции равнобедренного прямоугольного треугольника ABC (смотри задачу №1).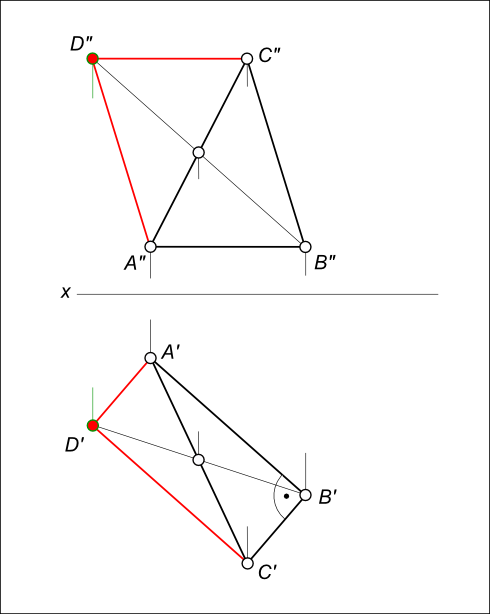
Построить фронтальную и горизонтальную проекции квадрата ABCD

Проекции прямоугольного треугольника

Построение квадрата заключается:
- в проведении AD // BC; - в проведении CD // AB.