Проекции ромба

Построить проекции ромба ABCD, исходя из следующих условий:
- диагональ ВD принадлежит прямой m(m`, m");
- вершина А(A`, ...) принадлежит прямой n(n`, n")=EF(E`F`, E"F");
- диагональ /АС/ = 2 /ВD/ (рис.).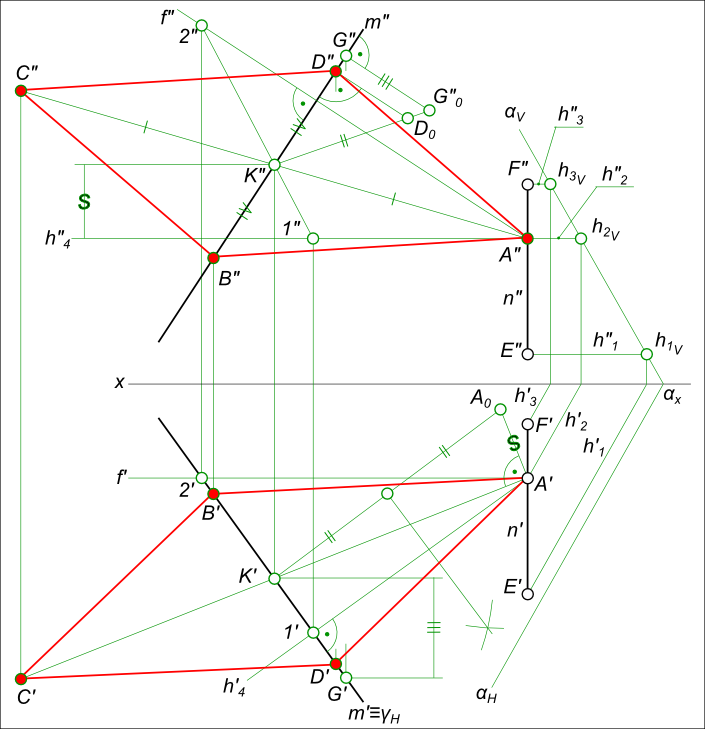

Проекции ромба

План решения задачи:
- построение недостающей проекции А" точки А ∈ n;
- А ∈ β(h₄ ∩ f) ⊥ m;
- К = β ∩ m;
- К ∈(АС) ⊥ m Λ /АК/ = /КС/;
- определяем истинные величины отрезков /АК/ и /КС/ способом прямоугольного треугольника;
- на прямой m от точки K откладываем отрезки /КВ/ = /КD/ = /AК// 2, используя способ прямоугольного треугольника;
- прямые (АС) и (ВС) перпендикулярны и делятся в точке пересечения пополам, следовательно, являются диагоналями ромба. Соединив одноименные проекции вершин прямыми линиями, получим искомые проекции ромба ABCD.

Построить проекции ромба ABCD, исходя из следующих условий:
- диагональ AC║п2 ;
- вершина B принадлежит п1;
- вершина D равноудалена от плоскостей проекции п1 и п2.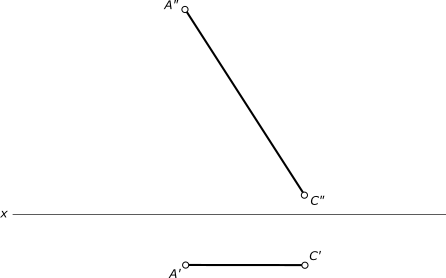

Проекции ромба

проекции ромба ABCD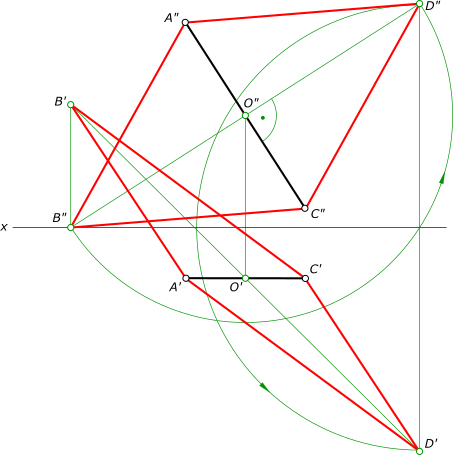

Проекции ромба

строим последовательно на основе анализа условия задачи.
1. Диагонали ромба взаимно перпендикулярны и точкой их пересечения делятся пополам:
- находим точку пересечения O(O`, O") диагоналей ромба разделив пополам диагональ AC.
- через точку O" проводим направление диагонали B"D" перпендикулярное A"C" до пересечения с осью x, где находим B" и затем D".
2. Из условия равного удаления точки D от п1 и п2:
- находим D`
3. Из условия принадлежности точки B плоскости п1:
- находим B` в пересечении направления диагонали O`D` и линии проекционной связи точки B.
4. Соединяем прямыми линиями найденные вершины B, D с вершинами AC и получаем искомые проекции ромба ABCD.

Проекции ромба построены также в статье Графическая работа 1