Проекция точки на плоскость в пространстве

Проекция точки на плоскость в пространстве будет построена, когда будет восстановлен перпендикуляр к данной плоскости, проходящий через точку и построена точка пересечения перпендикуляра с плоскостью:
Прямая и плоскость;
Пересечение прямой с плоскостью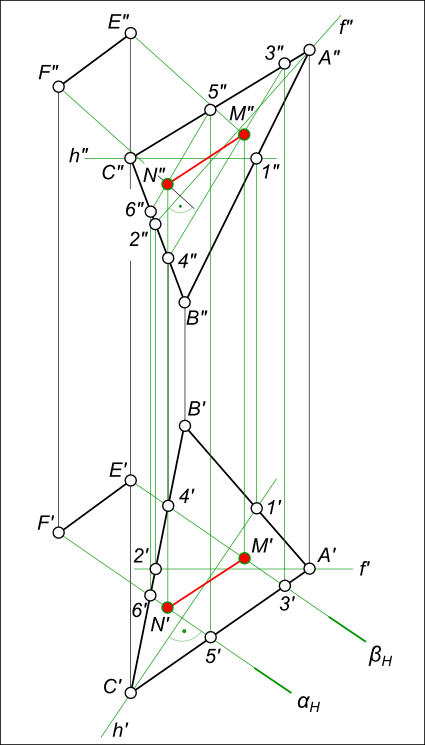

Проекция точки на плоскость в пространстве

Проекция точки на плоскость в пространстве будет построена, когда будет восстановлен перпендикуляр к данной плоскости, опущенный из точки на плоскость и построена точка пересечения перпендикуляра с плоскостью. Эти построения выполняются когда определяется расстояние от точки до плоскости способом прямоугольного треугольника.

Даны проекции: точки A(A`, A") и плоскости α(α_H, α_V). Найти расстояние от точки A до плоскости α способом прямоугольного треугольника.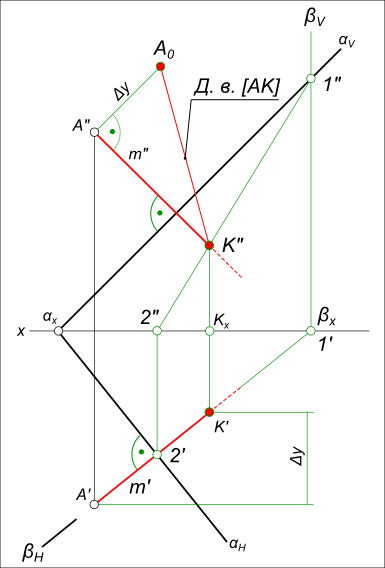

Проекция точки на плоскость в пространстве

Проекция точки на плоскость в пространстве строится в графической работе №2 задача №4 для двух точек отрезка EF: Графическая работа 2

Построить эпюр точки B симметричной A относительно прямой m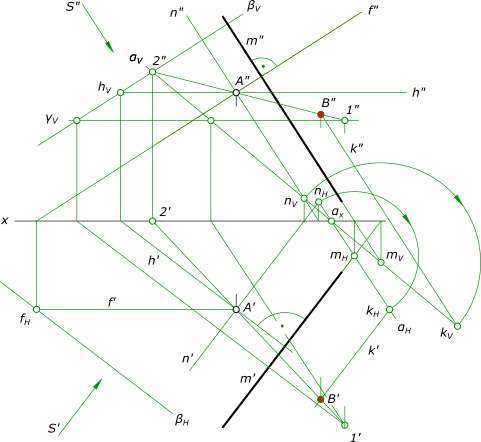

Проекция точки на плоскость в пространстве

Здесь показан один из многих путей решения данной задачи.
1. Используем косоугольное проецирование с направлением S параллельным заданной прямой m:
a) Через точку A проводим прямую n и находим следы nH, mH и nV, mV;
b) находим следы плоскости α по следам параллельных прямых ее образующих nH, mH и nV, mV;
c) находим следы kH и kV прямой k симметричной относительно прямой m на одноименных следах плоскости α.
2. Через точку A проводим плоскость β перпендикулярную параллельным прямым m, n и k плоскости α:
a) Через точку A проводим горизонталь и фронталь плоскости β;
b) Находим следы горизонтали и фронтали плоскости β;
c) Проводим следы плоскости β через следы ее горизонтали h и фронтали f.
3. Находим точку B встречи прямой k с плоскостью β:
a) Находим линию пересечения 1 - 2 плоскостей α и β;
b) Находим искомую точку B в пересечении линии 1-2 с прямой k.