Проекция точки на прямую

Проекция точки на прямую:
- заданную как пересечение двух плоскостей (b ∩ c) ∩ (d // e) = l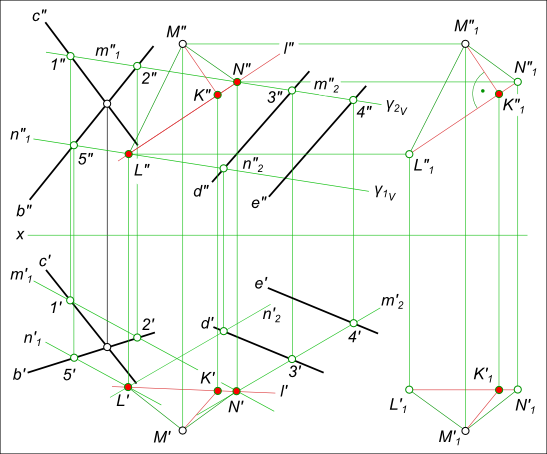

Проекция точки на прямую

построена с использованием:
- способа плоскопараллельного перемещения:
Способ плоскопараллельного перемещения;
Плоскопараллельное перемещение треугольника
- теоремы о проецировании плоского угла:
Прямые;
Проекции плоских углов.

На прямой m найти точку K равноудаленную от концов отрезка AB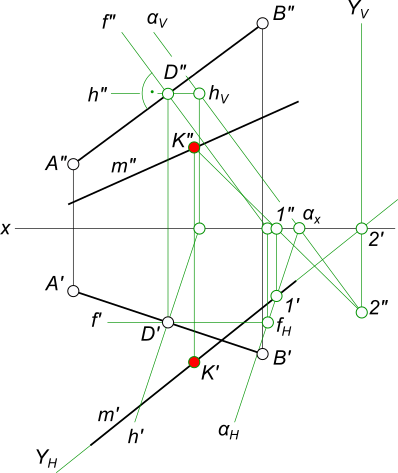

Проекция точки на прямую

В приведенной задаче также звучит тема проекция точки на прямую.
Первоначально вырабатываем план решения задачи, основанный на ряде соображений по условию задачи:
- на самом отрезке находим точку D, равноудаленную о его концов;
- точки равноудаленные от концов отрезка будут располагаться в плоскости α перпендикулярной ему и проходящей через точку D:
- проводим через точку D горизонталь h ⊥ m и фронталь f ⊥ m, затем находим αH и αV следы плоскости α;
- искомая точка K будет найдена в пересечении прямой m с плоскостью α:
- через прямую m проводим вспомогательную горизонтально проецирующую плоскость γ(γH, γV);
- строим линию пересечения 1-2 плоскостей α и γ;
- находим проекции искомой точки K сначала K" в пересечении прямой m" и 1"-2", затем K` в пересечении линии проекционной связи и m`.