Евклидово пространство и его свойства

Согласно теории множеств, любую геометрическую фигуру следует рассматривать как множество всех принадлежащих ей точек. Таким образом, всякая геометрическая фигура есть не пустое множество.
Отображение геометрической фигуры на плоскость (или какую-либо другую поверхность) можно осуществить путем проецирования ее точек на эту плоскость (поверхность).
Целесообразно рассмотреть евклидово пространство и его свойства до изучения метода проецирования.
Свойства евклидова пространства могут быть выражены при помощи системы предложений - аксиом, которые устанавливают зависимости и отношения между элементами пространства.
Точки, прямые и плоскости евклидова пространства (трехмерного) находятся в определенном взаимоотношении, которое может быть обозначено словом принадлежность или инцидентность.
Термин инцидентность заменяет такие понятия как лежать на, проходить через.
В дальнейшем вместо выражений точка лежит на плоскости, прямая проходит через точку мы будем употреблять:
- точка A принадлежит (инцидентна) плоскости;
- точка B принадлежит прямой.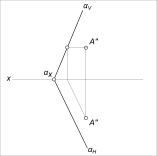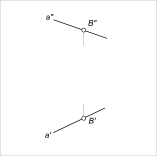

Евклидово пространство и его свойства

В символической форме эти выражения могут быть записаны

A ∈ α; B ∈ a

Аксиомы инцидентности или отношения принадлежности между элементами евклидова пространства могут быть выражены следующими предложениями:

1. Если точка A принадлежит прямой a, а прямая a принадлежит плоскости α, то точка A принадлежит плоскости α

2. Две различные точки A и B всегда принадлежат одной и той же и только одной прямой a или каждой прямой a принадлежат, по крайней мере, две точки A и B

3. Три различные точки A, B и C, не принадлежащие одной прямой, принадлежат одной и той же и только одной плоскости

4. Если две точки A и B, принадлежащие прямой a, принадлежат плоскости α, то и прямая a принадлежит плоскости α

Кроме отмеченных предложений, могут быть сформулированы и другие предложения принадлежности для элементов евклидова пространства:

5. Две прямые, принадлежащие одной плоскости, могут принадлежать одной точке, но этого может и не быть.

6. Две плоскости могут принадлежать одной и той же прямой, но этого может и не быть.

7. Плоскость и не принадлежащая ей прямая могут принадлежать одной точке, но этого может и не быть.

Последние три предложения по существу перефразируют аксиому о параллельности:
- предложение 5 утверждает, что в евклидовой плоскости две прямые либо пересекаются (принадлежат одной точке), либо не имеют общей точки,- в этом случае они называются параллельными;
- предложение 6 говорит о том, что в евклидовом пространстве две плоскости либо пересекаются (принадлежат одной прямой), либо они параллельны.
- предложение 7 утверждает, что в евклидовом пространстве прямая, не принадлежащая плоскости, либо пересекает ее (прямая и плоскость принадлежат одной точке), либо они параллельны.