Ортогональное проецирование

Ортогональное проецирование является частным случаем параллельного проецирования, при котором направление проецирования S перпендикулярно плоскости проекции α.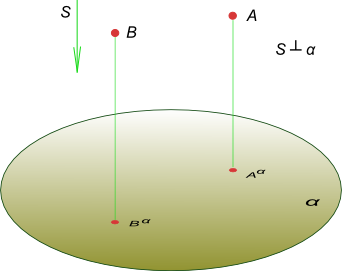

Ортогональное проецирование

Рисунок дает наглядное представление об ортогональным проецированием точки.

Кроме отмеченных ранее свойств параллельных проекций, для ортогонального проецирования будет справедлива следующая теорема:

для того чтобы прямой угол проецировался ортогонально без искажения, необходимо и достаточно, чтобы, по крайней мере, одна его сторона была параллельна плоскости проекции, а вторая сторона не перпендикулярна к этой плоскости.

Для доказательства этой теоремы обратимся к чертежу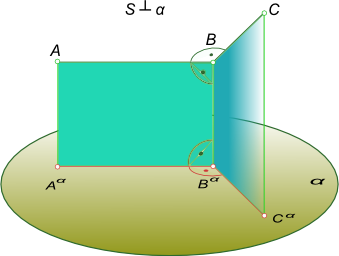

Ортогональное проецирование

В пространстве ABC = 90°, сторона AB данного угла параллельна плоскости проекции α, а сторона ВС не перпендикулярна этой плоскости, докажем, что A^αB^αC^α = 90°.

Фигура ABB^αA^α - прямоугольник, следовательно, AB перпендикулярен к проецирующей плоскости BCC^αB^α, так как он перпендикулярен к двум пересекающимся прямым этой плоскости (AB ⊥ BB^α по построению). Но AB║A^αB^α , Следовательно, A^αB^α⊥ плоскости BCC^αB^α, поэтому A^αB^α⊥B^αC^α, т. е. A^αB^αC^α = 90°.

Ортогональное проецирование обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием. Это: - простота геометрических построений для определения ортогональных проекций точек;
- возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры. При ортогональном проецировании если проецируемая фигура параллельна плоскости проекций, то ее проекция на данную плоскость не искажена или конгруентна проецируемой фигуре.
Отмеченные достоинства обеспечили широкое применение ортогонального проецирования, в частности, для составления машиностроительных чертежей.

Центральное и параллельное (косоугольное) проецирования позволяют однозначно решать задачу по определению проекции фигуры по заданному оригиналу, но не дают возможности воспроизвести (реконструировать) оригинал по его одной центральной или косоугольной проекции.
Для того чтобы получить ортогональный чертеж, обладающий свойством "обратимости", необходимо иметь, по крайней мере, две связанные между собой ортогональные проекции оригинала.