Свойства параллельного проецирования

Геометрические фигуры проецируются на плоскость проекции, в общем случае, с искажениями. Причем характер искажений проекций по сравнению с оригиналом зависит от аппарата проецирования и положения проецируемой фигуры по отношению к плоскости проекции. В частности, при параллельном проецировании нарушаются метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин). Действительно, пусть дана прямоугольная трапеция ABCD. Плоскость трапеции не параллельна плоскости проекции α. Определим параллельную проекцию при заданном направлении проецирования s.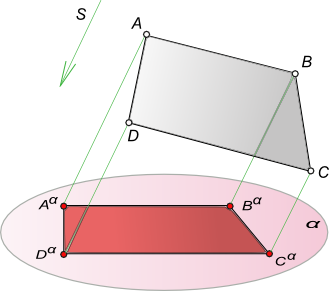

Свойства параллельного проецирования

Из рисунка видно, что проекция ABCD Существенно отличается от оригинала ABCD. Изменились длины сторон трапеции, другими стали величины углов при ее вершинах. При таких условиях, естественно, нарушается равенство площадей фигуры оригинала и ее проекции.

Наряду с этим, между оригиналом и его проекцией существует определенная связь, заключающаяся в том, что некоторые свойства оригинала сохраняются и на его проекции. Такие свойства принято называть проективными или инвариантными (независимыми) для данного способа проецирования.

Основу любой геометрии составляет система аксиом. Любые геометрические определения и предложения, равно как и доказательства теорем, базируются на принятой системе аксиом. В процессе параллельного проецирования (получения проекций геометрической фигуры по ее оригиналу) или реконструкции чертежа (воспроизведение оригинала по заданным его проекциям), любое определение, любую теорему можно составить и доказать, опираясь на инвариантные свойства параллельного проецирования, которые играют в начертательной геометрии такую же важную роль, как аксиомы в геометрии.

Таким образом, можно утверждать, что в начертательной геометрии существует, как бы, две системы аксиом:
- первая используется в процессе построения проекции геометрической фигуры по ее оригиналу. На этом этапе функции аксиом выполняют инвариантные свойства параллельного проецирования;
После того, как проекции определены, можно рассматривать задачу как плоскую, вступает в силу вторая система - аксиоматика евклидовой геометрии.

1. Проекция точки есть точка.

Это очевидно из самого определения проекции как точки пересечения проецирующего луча с плоскостью проекций.

2. Проекция прямой на плоскость есть прямая.

Действительно, при параллельном проецировании все лучи, проецирующие точки A,B,C,D,E прямой l, принадлежат одной плоскости Υ, параллельной направлению проецирования s. Эта плоскость пересекает плоскость проекции по прямой l^α. (Исходя из этого справедливо и следующее утверждение. Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций.)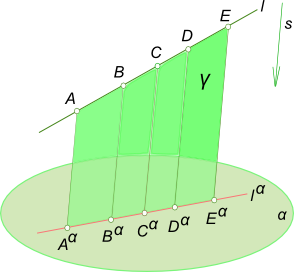

Свойства параллельного проецирования

3. Если в пространстве точка принадлежит (инцидентна) линии, то проекция этой точки принадлежит проекции линии. Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.

4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.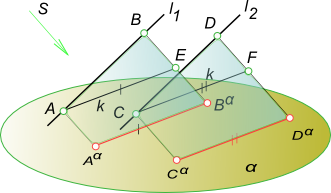

Свойства параллельного проецирования

Если [AB]║[CD], то плоскости ABB^αA^α и CDD^αC^α параллельны как имеющие углы при вершинах B и D с соответственно параллельными сторонами - (BA)║(DC) и (BB^α)║(DD^α). Эти плоскости пересекаются плоскостью проекции α по параллельным прямым l^α₁║l^α₂. Проведем в проецирующей плоскости ABB^αA^α через точку A прямую k₁║l₁, а в плоскости CDD^αC^α прямую k₂║l₂. Эти прямые пересекут проецирующие лучи [BB^α) и [DD^α) в точках E и F. Отрезок [AE] [A^αB^α], а [CF] [C^αF^α] как отрезки параллельных между параллельными. ΔABE подобен ΔCDF. На основании подобия треугольников можно записать:

Из четвертого свойства следует:

а) если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией этой точки в том же отношении.

Доказательство этого свойства аналогично предыдущему, понятно из чертежа на рисунке и не требует дополнительных пояснений.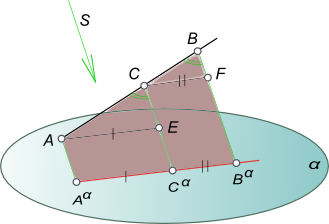

Свойства параллельного проецирования

Как следствие пункт a) можно записать: середина отрезка оригинала проецируется в середину его проекции. Поэтому медианы треугольника проецируются в медианы его проекций, а следовательно, центр тяжести треугольной пластинки проецируется в центр тяжести треугольника - проекций; центр окружности, как точка, делящая все диаметры пополам, проецируется в центр эллипса. Взаимно перпендикулярные диаметры окружности проецируются в сопряженные диаметры эллипса.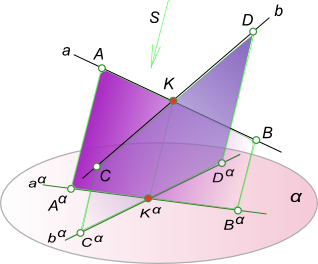

Свойства параллельного проецирования

б) Проекции конгруентных отрезков взаимно параллельных прямых взаимно параллельны и конгруэнтны.

Поэтому проекцией любого параллелограмма будет параллелограмм. В параллелограммы проецируется также произвольно расположенный по отношению к плоскости проекции прямоугольник, ромб, квадрат.

5. Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых. Пусть две прямые a и b пересекаются в точке K. Так как точка K принадлежит прямой a, то на основании свойства 3 K^α ∈ a^α. Одновременно K ∈ b, следовательно, K^α ∈ b^α. Эти два условия могут быть удовлетворены только в том случае, если K^α будет точкой пересечения проекций прямых a и b.

6. Плоская фигура, параллельная плоскости проекции, проецируется на эту плоскость в конгруентную фигуру.

7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.

Следствием этого свойства будут:
- плоская ломанная линия проецируется, в общем случае, в ломанную линию с тем же числом вершин;
- плоская кривая проецируется, в общем случае, в кривую линию;
- проекция в виде отрезка прямой не определяет оригинала, которым могут быть: прямая, плоская ломанная или кривая линии, любая плоская фигура.

8. Параллельный перенос оригинала или плоскости проекции не изменяет вида и размеров проекции оригинала.