Положение точки в пространстве

Положение точки в пространстве (а следовательно, и любой геометрической фигуры) может быть определено, если будет задана какая-либо координатная система отнесения.
Положение точки в пространстве, геометрической фигуры наиболее удобно для фиксирования и выявления ее формы по ортогональным проекциям в декартовой системе координат, состоящей из трех взаимно перпендикулярных плоскостей.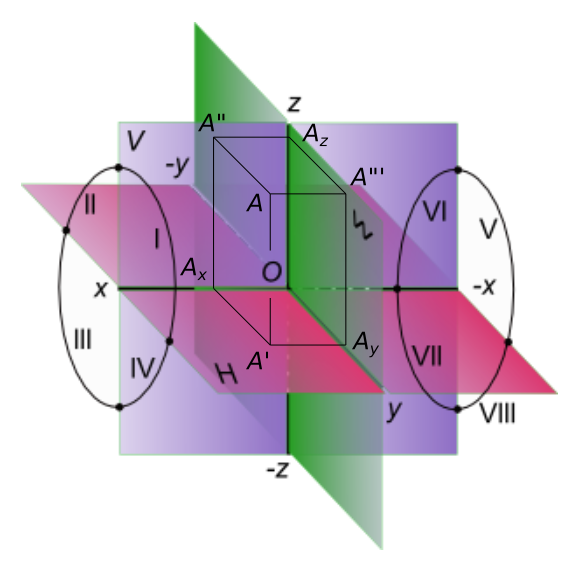

Положение точки в пространстве

При ортогональном проецировании точки А получаем:
А`– проекция точки А на плоскость H (горизонтальная проекция точки А);
А"– проекция точки А на плоскость V (фронтальная проекция точки А);
А"`– проекция точки А на плоскость W (профильная проекция точки А);
Координатой точки называется удаление точки от плоскости проекции:
Для задания положения точки А(x,y,z) необходимы:
- или три координаты x,y и z;
- или две проекции A`(x;y) и A"(x;z), или A`(x;y) и A"`(y;z), или A"(x;z) и A"`(y;z).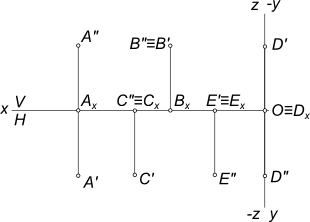

Положение точки в пространстве

Положение точки в пространстве может быть задано графически путем указания двух ее проекций - A`(x;y) и A"(x;z) здесь имеются все три координаты точки A. Линия соединяющая на эпюре проекции точки называется линией проекционной связи. Если координаты точки ≠ 0, то это точку называют точкой общего положения, если 1 или 2 координаты = 0, то точка называется точкой частного положения. На представленном рисунке:
- точки A и B общего положения, кроме того точка B принадлежит биссекторной плоскости;
- точки частного положения:
- точка CED принадлежит горизонтальной плоскости проекций H;
- точка E принадлежит фронтальной плоскости проекций V;
- точка D принадлежит профильной плоскости проекций W;