Принадлежность прямой плоскости

Принадлежность прямой плоскости на комплексном чертеже определяется согласно аксиомам инцидентности или отношения принадлежности между элементами евклидова пространства, которые гласят: - если точка A принадлежит прямой k, а прямая k принадлежит плоскости α, то точка A принадлежит плоскости α;
- если две точки A и B, принадлежащие прямой k, принадлежат плоскости α, то и прямая k принадлежит плоскости α.

Задача на принадлежность прямой плоскости может быть выражена следующим образом:
- заключить прямую k(k`, k") в;
- провести через прямую k(k`, k")
плоскость α общего положения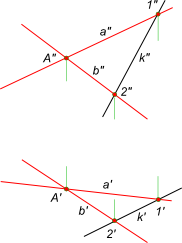

Принадлежность прямой плоскости

Положение плоскости α в пространстве определяется тремя точками:
- точка A ∉ k;
- точки 1 и 2 ∈ k
Здесь принадлежность прямой плоскости α общего положения определяется двумя точками - 1 и 2 взятыми на прямой k.
Проведя прямые через точки 1 и A и 2 и A получим искомую плоскость , заданную пересекающимися прямыми a и b соответственно.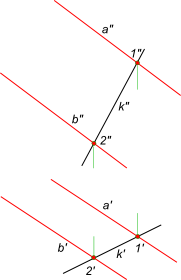

Принадлежность прямой плоскости

Положение плоскости α в пространстве определяется двумя параллельными прямыми:
- a // b и точки 1 ∈ a и 2 ∈ b
- точки 1 и 2 ∈ k
Здесь принадлежность прямой плоскости α общего положения определяется двумя точками - 1 и 2 взятыми на прямой k.
Проведя прямые a // b через точки 1 и 2 соответственно получим искомую плоскость , заданную прямыми a // b.

Провести через прямую k(k`, k") плоскость α общего положения, заданную следами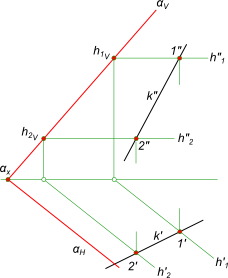

Принадлежность прямой плоскости

Положение плоскости α в пространстве определяется двумя параллельными прямыми - горизонталями плоскости:
- h₁ // h₂ и точки 1 ∈ h₁ и 2 ∈ h₂
- точки 1 и 2 ∈ k
Здесь принадлежность прямой плоскости α общего положения определяется двумя точками - 1 и 2 взятыми на прямой k.
Проведя прямые h₁ // h₂ через точки 1 и 2 соответственно, получим искомую плоскость α, заданную следами α_H и α_V.