Положение точки в пространстве

Положение точки в пространстве представим с помощью пространственного макета. Пусть даны в пространстве точка A и три взаимно перпендикулярные плоскости проекции.

Построим проекции точки А, расположенной в первом октанте пространства. Для этого через точку проведем проецирующие лучи, идущие перпендикулярно плоскостям проекций . На пересечении этих лучей с плоскостями проекций H, V, W находятся проекции самой точки А (A`, A", A"`).

Положение точки в пространстве

Положение точки в пространстве определяется тремя координатами (x, y, z), показывающими величины расстояний, на которые она удалена от плоскостей проекций.
Чтобы определить эти расстояния, достаточно через точку A провести прямые, перпендикулярные к плоскостям проекций, определить точки A`, A", A"` встречи этих прямых с плоскостями проекций и измерить величины отрезков [AA`], [AA"], [AA"`], которые укажут соответственно значение аппликаты z, ординаты y, абсциссы x точки A.

Точки A`, A", A"` называют ортогональными проекциями точки A, при этом согласно принятым обозначениям:
A` - горизонтальная проекция точки A;
A" - фронтальная проекция точки A;
A"` - профильная проекция точки A.

Отрезки:
[AA`] - [OA<sub>x</sub>] - абсцисса точки A;
[AA"] - [OA<sub>y</sub>] - ордината точки A;
[AA"`] - [OA_z] - аппликата точки A.

Прямые (AA` ⊥ H), (AA" ⊥ V), (AA"` ⊥ W) называют проецирующими прямыми или проецирующими лучами.
Прямую (AA`), проецирующую точку A на горизонтальную плоскость проекций, называют горизонтально проецирующей прямой (лучом).
Прямую (AA") проецирующую точку A на фронтальную плоскость проекций называют фронтально проецирующей прямой (лучом).
Прямую (AA"`) проецирующую точку A на профильную плоскость проекций называют профильно-проецирующей прямой (лучом).
Две проецирующие прямые, проходящие через точку A, определяют плоскость, которую принято называть проецирующей.

Чтобы получить эпюр точки A, выполним преобразование пространственного макета в эпюр Монжа:
- фронтальная проекция точки A остается на месте, как принадлежащая плоскости V, которая не меняет своего положения при рассматриваемом преобразовании.
- горизонтальная проекция A` вместе с горизонтальной плоскостью проекции опустится вниз и расположится на одном перпендикуляре к оси x с фронтальной проекцией A".
- профильная проекция AA"` будет вращаться вместе с профильной плоскостью проекции и к концу преобразования займет положение, указанное на рисунке. При этом AA"` будет принадлежать перпендикуляру к оси z, проведенному через A" и удалена от оси z на такое же расстояние, на какое горизонтальная проекция A` удалена от оси x.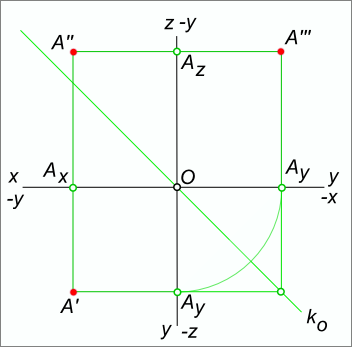

Положение точки в пространстве

Связь между горизонтальной и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков [A`A<sub>y</sub>] и [A<sub>y</sub>A"`] и сопрягающей их дуги окружности, с центром в точке пересечения координатных осей.
Отмеченной связью пользуются для нахождения недостающей профильной или горизонтальной проекции.

Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено и без проведения дуги окружности. В этом случае связь между горизонтальной и профильной проекциями может быть установлена с помощью ломаной линии A`,A<sub>o</sub>,A"` с вершиной A_o на биссектрисе угла, образованного осями y.
Биссектрису O,A_o,A"` называют постоянной прямой k_o эпюра Монжа.

Представленная на рисунке плоская модель (эпюр) несет такую же информацию, какая содержится в пространственном макете.
Действительно: чтобы определить положение точки в пространстве, необходимо знать три координаты точки A - (x, y, z) - это длины отрезков [AA"`], [AA"], [AA`].
Величины этих отрезков могут быть легко определены на эпюре:
[AA"`] ≅ [A`A_y] ≅ [A"A_z];
[AA"] ≅ [A`A<sub>x</sub>] ≅ [A"`A_z];
[AA`] ≅ [A"A<sub>x</sub>] ≅ [A"`A_y].

Горизонтальная проекция точки A определяется абсциссой x и ординатой y
Фронтальная проекция - абсциссой x и аппликатой z
Профильная проекция - ординатой y и аппликатой z

A[A`(x, y); A"(x, z); A"`(y, z)]

Из записи следует:
1. Точка в пространстве удалена:
а) от плоскости проекции W на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси y (или же фронтальная проекция A" от оси z);
б) от плоскости проекции V на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси x (или ее профильная проекция A"` от оси z);
в) от плоскости проекции H на такую же величину, на какую ее фронтальная проекция A" удалена от оси x (или ее профильная проекция A"` от оси y).

2. Положение точки в пространстве вполне определяется положением ее двух ортогональных проекций.
Как следствие из этого - по двум любым заданным ортогональным проекциям точки всегда можно построить недостающую ее третью ортогональную проекцию.
Действительно: какое бы сочетание из двух ортогональных проекций мы не взяли, они всегда дают нам значение всех трех координат точки.
3. a) горизонтальная и фронтальная проекции любой точки принадлежат одному перпендикуляру к оси x.

Если принять во внимание, что на эпюре прямые, перпендикулярные к осям проекций и соединяющие разноименные проекции точек, называют линиями связи (проекционной связи), то пункт 3. а) может быть сформулирован иначе:
горизонтальная и фронтальная проекции любой точки принадлежат одной линии связи.

б) горизонтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси y;
в) фронтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси z.