Взаимно перпендикулярные прямые

Взаимно перпендикулярные прямые - это прямые пересекающиеся под прямым углом. Построить взаимно перпендикулярные прямые бывает необходимо для решения той или иной задачи. Например в задаче на определение расстояния от точки до прямой.
Наглядное пространственное представление графического решения задачи на построение взаимно перпендикулярных прямых дает рисунок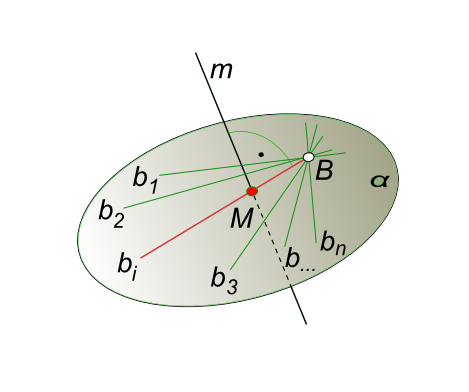

Взаимно перпендикулярные прямые

Через точку B можно провести множество прямых {b1, b2, ..., bn}, перпендикулярных к прямой m. Это множество прямых определяет плоскость α ⊥ m.
Чтобы выделить из {b1, b2, ..., bn} единственную прямую bi, пересекающую данную прямую m и следовательно взаимно перпендикулярную к ней, необходимо:
- Найти точку встречи прямой m с плоскостью α. M = m ∩ α;
- Зная положение точки M, провести через нее прямую bi и определить действительную величину отрезка [BM], выражающую искомое расстояние от точки до прямой.
На основе выше приведенного рисунка может быть решена задачи по построению перпендикулярных прямых которые не пересекаются, трех взаимно перпендикулярных прямых.

Прямой угол между двумя пересекающимися прямыми проецируется без искажения, если хотя бы одна из прямых параллельна плоскости проекций.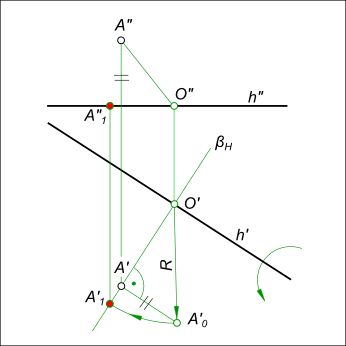
Найти расстояние от точки A до прямой h. Решение подобной задачи предполагает, что будут построены взаимно перпендикулярные прямые

Взаимно перпендикулярные прямые

Для определения натуральной величины отрезка перпендикуляра от точки A до прямой h используем способ вращения вокруг горизонтали:
- через точку A проводим горизонтально проецирующую плоскость β_H ⊥ h` и на их пересечении находим O` и по линии связи O" - проекции центра вращения;
- определяем действительную величину радиуса вращения R=[O`A`₀], применив способ прямоугольного треугольника;
- описываем дугу радиуса R до пересечения с β_H и находим точку A`<sub>1</sub> и расстояние от точки A до прямой h в виде отрезка [A`₁O`] ⊥ h`.
[AO] ⊥ h - это прямые пересекающиеся под прямым углом - взаимно перпендикулярные прямые.

Для того чтобы построить взаимно перпендикулярные прямые, в случае когда одна из них задана прямой общего положения, необходимо перевести ее, предварительно, в положение либо горизонтали, либо фронтали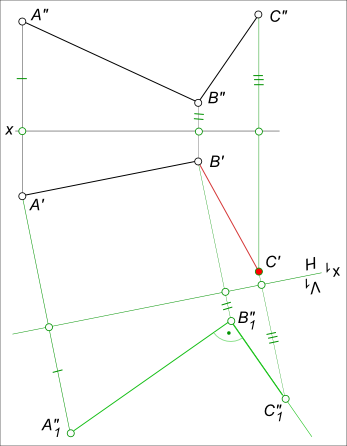

Взаимно перпендикулярные прямые

Здесь построение второй стороны прямого угла выполняется способом перемены плоскости проекции. Вводится новая фронтальная плоскость проекции V₁, для которой сторона AB прямого угла есть фронтальная прямая. И тогда прямой угол ABC проецируется на V₁ без искажения. Аппликата точки C при перемене плоскости V на V₁ остается неизменной и ее пресечение с направлением стороны BC дает положение искомой точки C₁. Искомую проекцию C` находим на пересечении линий связи точки C.

Та же задача на взаимно перпендикулярные прямые может быть решена по другим способом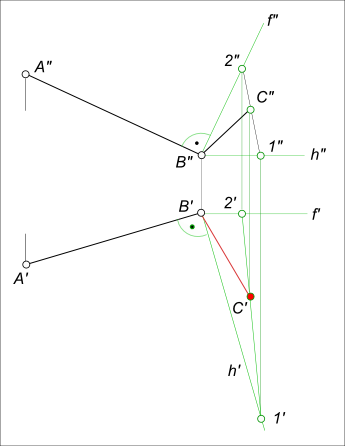

Взаимно перпендикулярные прямые

Здесь сторона BC, заключается в плоскость перпендикулярную второй стороне прямого угла AB. Затем в этой плоскости проводится прямая 1 - 2 через точку C и находится горизонтальная проекция C`, как принадлежащая прямой 1` - 2`.