Линия пересечения поверхностей многогранников

Линия пересечения поверхностей многогранников может быть построена способом вспомогательных секущих плоскостей, которые могут быть проецирующими или общего положения.
В случае проецирующего положения поверхностей одного из многогранников по отношению к плоскостям проекций, точки пересечения можно получить без выполнения каких либо построений на одной из проекций, а затем по линиям проекционной связи найти их недостающие проекции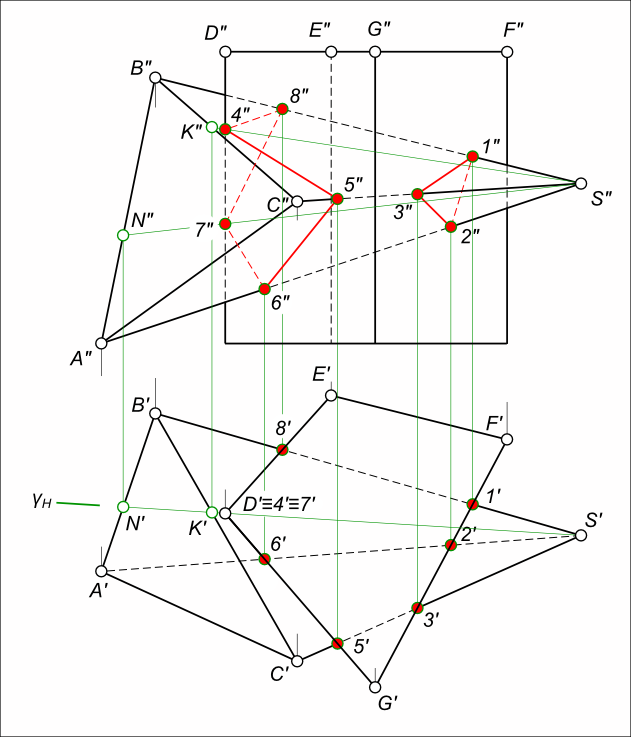

Линия пересечения поверхностей многогранников

Таким образом, находим точки 1, 2, 3, 5, 6 и 8 пересечения поверхностей двух многогранников прямой призмы EFGD и пирамиды SABC.
Для нахождения точек 4 и 7 пересечения поверхностей многогранников вводим вспомогательную поверхность - плоскость γ_H, проходящую через ребро D призмы и вершину S пирамиды. Плоскость γ_H пересечет грани пирамиды SBC и SAB по прямым SK и SN соответственно, которые пересекаясь с ребром D призмы дадут искомые точки 4 и 7 пересечения этого ребра с указанными гранями пирамиды.

Найденные точки:
- 1, 2, 3 и соединяем прямыми линиями, они образуют плоскую замкнутую ломаную линию, потому что принадлежат одной грани FG призмы;
- 4, 5, 6, 7 и 8 соединяем прямыми линиями, они образуют пространственную замкнутую ломаную линию, потому что принадлежат граням GD и ED призмы.

Линия пересечения поверхностей многогранников показывается на эпюре красным цветом с учетом ее видимости на проекциях. Невидимые части линии отображают штрихпунктирной линией.

Графическая работа 7:
построена линия пересечения поверхностей многогранников в прямоугольной диметрии;
построена развертка поверхностей многогранников с отображением на них их линии пересечения.