Способ вспомогательных секущих плоскостей

Способ вспомогательных секущих плоскостей позволяет определять линии пересечения различных поверхностей. Наиболее простые решения имеют место при пересечении линейчатых поверхностей.
Даны две произвольные конические поверхности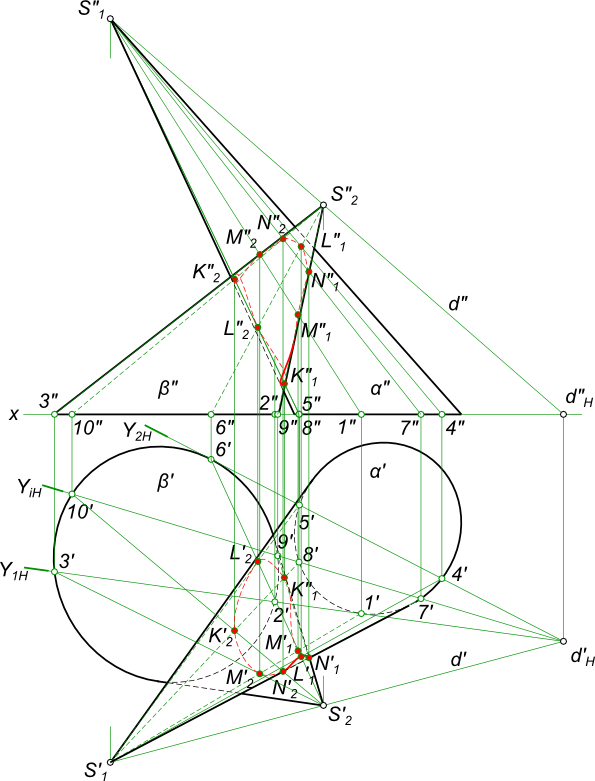

Способ вспомогательных секущих плоскостей

требуется построить линию пересечения поверхностей данных конусов.
Коническая поверхность пересекается плоскостью по прямым образующим, в случае если она (плоскость) проходит через вершину конической поверхности. Для нахождения точек линии пересечения заданных конических поверхностей α и β необходимо провести секущую плоскость Y1 через их вершины S1 и S2. Секущая плоскость Y1, Y2 и Yi пересечет конические поверхности:
- α по прямым S₁1;
- β по прямым S₂2 и S₂3.
Аналогично секущие плоскости Y2 и Yi пересекают конические поверхности.
Пересечения прямых - точки:
M1=S₁1∩S₂2;
M2=S₁1∩S₂3;
L1=S₁4∩S₂6;
L1=S₁5∩S₂6;
K1=S₁7∩S₂9;
K2=S₁8∩S₂10;
N1=S₁7∩S₂9;
N2=S₁8∩S₂10
принадлежат искомой линии пересечения поверхностей.
Для построения линии пересечения поверхностей на эпюре, в первую очередь, необходимо определить опорные точки, которые получаются при сечении поверхностей α и β плоскостями, касательными к одной или двум из этих поверхностей.
Горизонтальные следы этих плоскостей Y1H и Y2H определяют угол Y1HdHY2H, в пределах которого следует проводить горизонтальные следы вспомогательных секущих плоскостей.

Даны произвольные цилиндрическая и коническая поверхности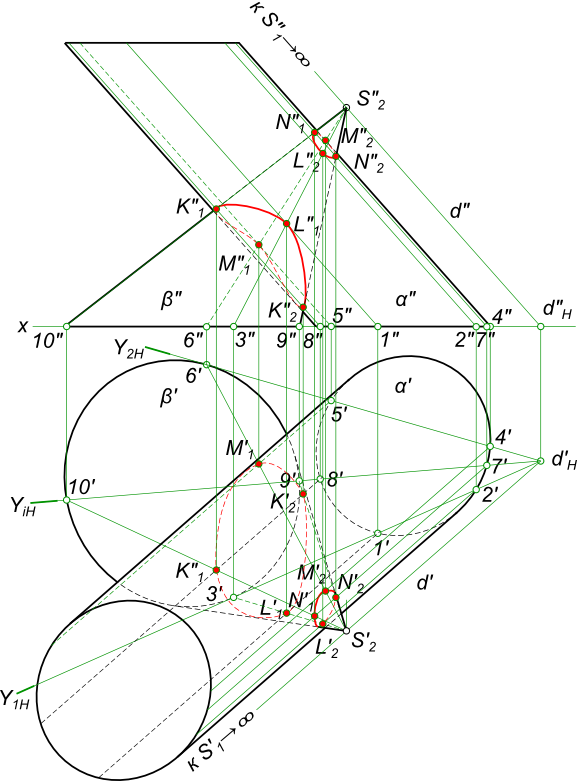

Способ вспомогательных секущих плоскостей

требуется построить линию пересечения поверхностей данных цилиндра и конуса.
Коническая поверхность пересекается плоскостью по прямым образующим, в случае если она (плоскость) проходит через вершину конической поверхности.
Цилиндрическая поверхность пересекается плоскостью по прямым образующим, в случае если она (плоскость) проходит через вершину конической поверхности. Здесь цилиндрическая поверхность рассматривается как коническая поверхность имеющая свою вершину в не собственной точке (удаленной в бесконечность)
Для нахождения точек линии пересечения заданных конических поверхностей α и β необходимо провести секущую плоскость Y1 через их вершины S1 и S2. Секущая плоскость Y1, Y2 и Yi пересечет конические поверхности:
- α по прямым S₁1;
- β по прямым S₂2 и S₂3.
Аналогично секущие плоскости Y2 и Yi пересекают конические поверхности.
Пересечения прямых - точки:
M1=S₁1∩S₂2;
M2=S₁1∩S₂3;
L1=S₁4∩S₂6;
L1=S₁5∩S₂6;
K1=S₁7∩S₂9;
K2=S₁8∩S₂10;
N1=S₁7∩S₂9;
N2=S₁8∩S₂10
принадлежат искомой линии пересечения поверхностей.
Для построения линии пересечения поверхностей на эпюре, в первую очередь, необходимо определить опорные точки, которые получаются при сечении поверхностей α и β плоскостями, касательными к одной или двум из этих поверхностей.
Горизонтальные следы этих плоскостей Y1H и Y2H определяют угол Y1HdHY2H, в пределах которого следует проводить горизонтальные следы вспомогательных секущих плоскостей.

Даны произвольные цилиндрические поверхности α и β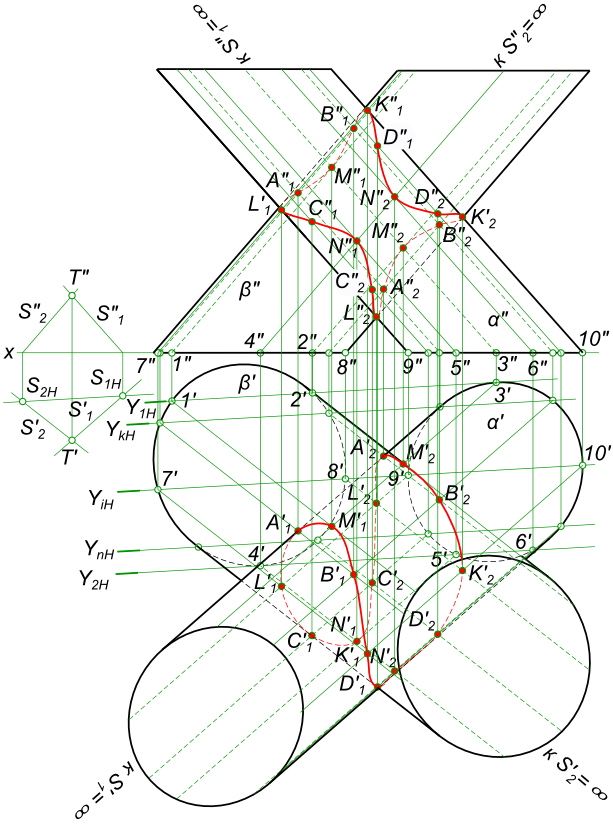

Способ вспомогательных секущих плоскостей

требуется построить линию пересечения поверхностей данных цилиндров α и β.
Здесь цилиндрические поверхности рассматривается как конические с вершинами в несобственной точке S1=∞ и S2=∞. Коническая поверхность пересекается плоскостью по прямым образующим, в случае если она (плоскость) проходит через вершину конической поверхности.
Цилиндрическая поверхность пересекается плоскостью по прямым образующим, в случае если она (плоскость) проходит через вершину конической поверхности. Здесь цилиндрическая поверхность рассматривается как коническая поверхность имеющая свою вершину в не собственной точке (удаленной в бесконечность)
Для нахождения точек линии пересечения заданных конических поверхностей α и β необходимо провести секущую плоскость Y1 через их вершины S1 и S2. Секущая плоскость Y1, Y2 и Yi пересечет конические поверхности:
- α по прямым S₁1;
- β по прямым S₂2 и S₂3.
Аналогично секущие плоскости Y2 и Yi пересекают конические поверхности.
Пересечения прямых - точки:
M1=S₁1∩S₂2;
M2=S₁1∩S₂3;
L1=S₁4∩S₂6;
L1=S₁5∩S₂6;
K1=S₁7∩S₂9;
K2=S₁8∩S₂10;
N1=S₁7∩S₂9;
N2=S₁8∩S₂10
принадлежат искомой линии пересечения поверхностей.
Для построения линии пересечения поверхностей на эпюре, в первую очередь, необходимо определить опорные точки, которые получаются при сечении поверхностей α и β плоскостями, касательными к одной или двум из этих поверхностей.
Горизонтальные следы этих плоскостей Y1H и Y2H определяют угол Y1HdHY2H, в пределах которого следует проводить горизонтальные следы вспомогательных секущих плоскостей.