Способ вспомогательных секущих сферических поверхностей

Способ вспомогательных секущих сферических поверхностей позволяет определять линию пересечения двух произвольных поверхностей вращения.
Для этого используется свойство присущее поверхностям вращения - две любые соосные поверхности вращения пересекаются по окружности, проходящей через точки (A, B) пересечения их меридианов (m1, m2).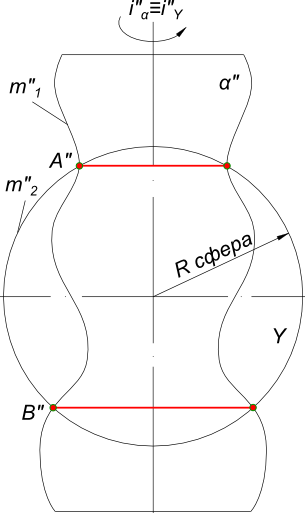

Способ вспомогательных секущих сферических поверхностей

Плоскости окружностей сечения перпендикулярны оси поверхности вращения. Поэтому, если оси поверхностей вращения параллельны плоскости проекции, то на эту плоскость окружности сечения проецируются в отрезки прямых, перпендикулярных проекции на нее оси вращения.
В качестве вспомогательной секущей поверхности вращения используют удобную для вычерчивания сферическую поверхность, центр которой должен принадлежать оси поверхности вращения.
Задачи по определению линии пересечения двух произвольных поверхностей вращения, имеющих общую плоскость симметрии просто решаются с помощью вспомогательных сферических поверхностей.
При этом различают два случая:
- если оси поверхностей пересекаются;
- если оси поверхностей не пересекаются.

Оси двух произвольных поверхностей вращения пересекаются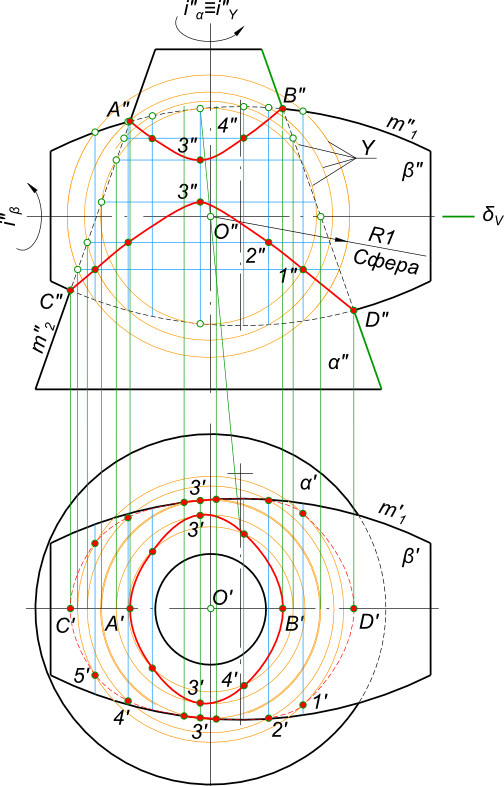

Способ вспомогательных секущих сферических поверхностей

определение линии пересечения двух поверхностей вращения выполняют с помощью концентрических сфер.
В данном примере это конус и тороид (самопересекающийся тор),
используется способ вспомогательных секущих сферических поверхностей, которые имеют общий центр.
Применение концентричных сфер возможно при наличии трех графических условий:
- пересекаются поверхности вращения (за исключеним открытого и закрытого тора);
- общая плоскость симметрии представляет собой плоскость уровня;
- оси поверхостей пересекаются в точке, которая служит общим центром вспомогательных секущих сферических поверхностей.
Способ вспомогательных секщих плоскостей тут применять не рационально, так как ни одна плоскость уровня не пересекает поверхности по окружностям.
Алгоритм построения линии пересечения:
- находим опорные точки A и B, C и D в пересечении меридиональных сечений m1 и m2 поверхностей α и β;
- находим точку пересечения осей поверхностей α и β: О=(iα ∩ iβ);
- проводим вспомогательную сферическую поверхность Y произвольным радиусом Р, которая пересечет пересечет поверхности α и β по окружностям a=(α ∩ Y) и b=(β ∩ Y) соответственно;
- находим точки линии пересечения в пересечении окружностей;
- действуя подобным образом, можно найти достаточное количество точек, соединив которые плавной линией получим искомую линию пересечения поверхностей.

Когда оси поверхностей не пересекаются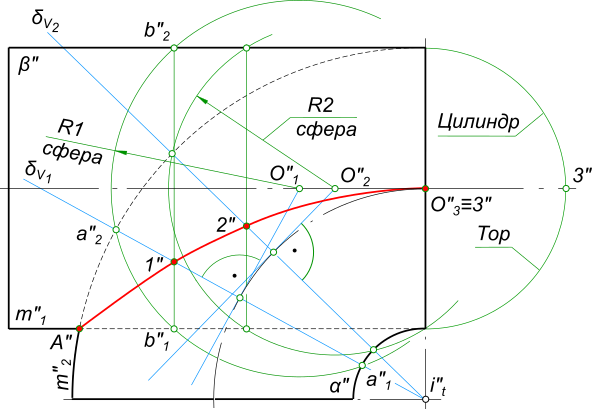

Способ вспомогательных секущих сферических поверхностей

Построение линии пересечения открытого тора и цилиндра выполняется способом эксцентричных сфер так как:
- открытый тор имеет круговые сечения во фронтально-проецирующих плоскостях, проходящих через его ось вращения i_t;
- общая плоскость симметрии поверхностей;
- оси поверхностей скрещиваются

и ведется по следующему алгоритму:
- вводим вспомогательные сферы, задавая произвольные сечения поверхности тора фронтально проецирующими плоскостями, проходящими через его ось. Окружность a1-a2 - это заданная линия пересечения тора с искомой вспомогатнльной сферой, центр которой должен лежать на перпендикуляре к проекции этой окружности;
- проводим к прямой a1-a2 через ее середину перпендикуляр к и на его пересечении с осью цилиндра находим центр O1 вспомогательной сферы;
- из центра O1 проводим окружность радиусом Rсф1;
- строим линию пересечения сф1 с цилиндром b1-b2;
- в пересечении a1-a2 и b1-b2 находим совпадающие точки 1(1);
- действуя подобным образом, можно найти достаточное количество точек, соединив которые плавной линией получим искомую линию пересечения поверхностей.