Принадлежность точки поверхности

Принадлежность точки поверхности может быть определена по эпюру Монжа.

Для точки A задача на принадлежность точки поверхности α может иметь три варианта задания:
- принадлежит ли точка, заданная своими проекциями, данной поверхности;
- на данных ортогональных проекциях поверхности α указать проекции произвольной точки A ∈ α;
- по положению одной известной проекции точки A ∈ α, построить недостающую ее проекцию.

Решение задачи на принадлежность точки поверхности выполняется по одному, для всех вариантов, алгоритму в основу которого полржено одно из главных свойств ортогонального проецирования - если точка принадлежит линии, то ее проекции принадлежат одноименным проекциям линии:

Из этого утверждения вытекает другое, более общее - если точка принадлежит поверхности, то она принадлежит какой либо линии данной поверхности. у этого утверждения имеется и обратное значение:

По эпюру Монжа принадлежность точки поверхности α будет установлена если A` ∈ k` и A" ∈ k" Λ k` ∈ α` и k" ∈ α", то точка A ∈ α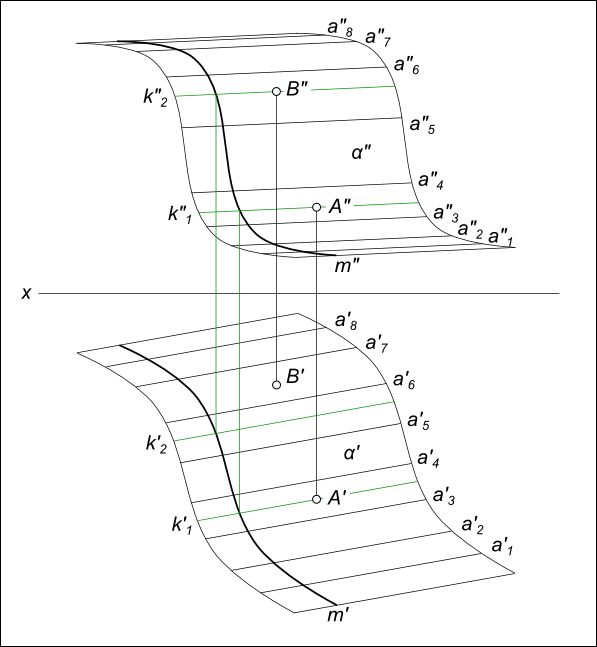

Принадлежность точки поверхности

Поверхность α образована перемещением прямой линии a по произвольной линии m. Необходимо установить принадлежность точки поверхности α: для A и B.
Проверка производится построением прямых принадлежащих поверхности α:
k"1 ∋ A";
k"2 ∋ B";
k`1 ∋ A`;
B` ∉ k`2, следовательно точка B ∉ α.