Прямой правильной призмы

Решение задачи на принадлежность точки поверхности прямой правильной призмы выполняется по алгоритму в основу которого положено одно из главных свойств ортогонального проецирования - если точка принадлежит линии, то ее проекции принадлежат одноименным проекциям линии.
Из этого утверждения вытекает другое, более общее - если точка принадлежит поверхности, то она принадлежит какой либо линии данной поверхности. У этого утверждения имеется и обратное значение.

Принадлежность точки поверхности прямой правильной призмы устанавливается по их принадлежности ребрам и граням этой призмы.
Построить горизонтальные и профильные проекции точек D, E, F и K, принадлежащих боковой поверхности призмы и заданных фронтальными проекциями - D", E", F" и K".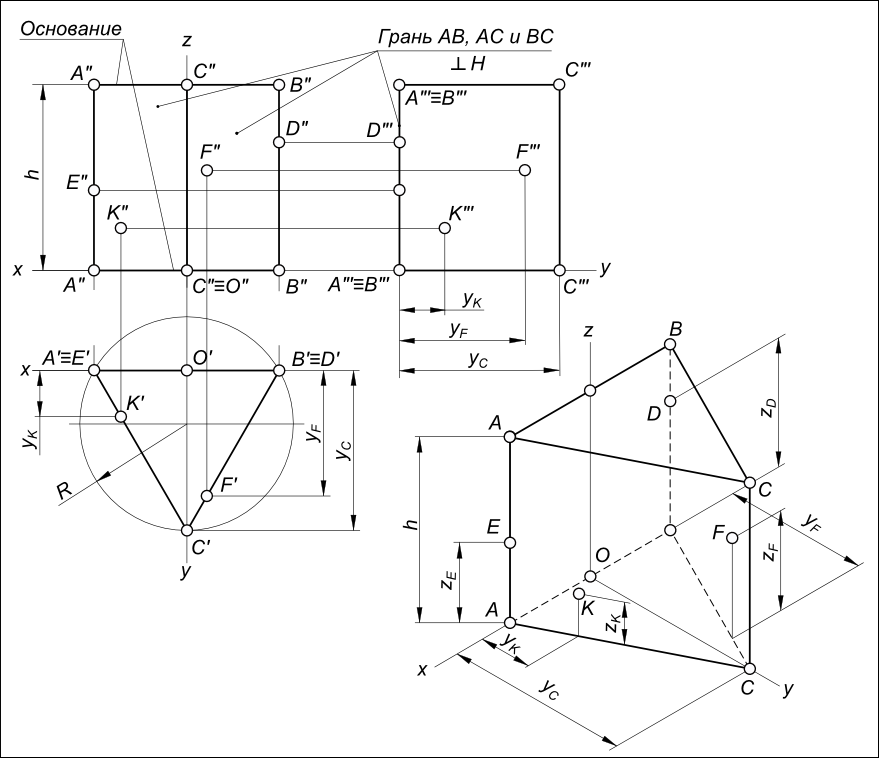

Прямой правильной призмы

Горизонтальные проекции E` и D` точек E и D принадлежащих ребрам A и B совпадают с их горизонтальными проекциями A` и B` в силу третьего инварианта параллельного проецирования.
Профильные проекции E"` и D"` точек E и D найдены по их принадлежности ребрам A и B соответственно.

Горизонтальные проекции K` и F` точек K и F принадлежащих граням AС и BС находятся на стронах A`C` и C`B` треугольника A`B`C`, которые представляют собой горизонтальные проекции этих граней.
Профильные проекции K"` и F"` точек E и D найдены координатным способом:
для точки K"` откладываем yK по линии проекционной связи;
для точки F"` откладываем yF по линии проекционной связи.

Прямоугольная изометрическая проекция прямой правильной призмы и точек на ее боковой поверхности так же показаны на рисунке.