Сечение призмы плоскостью

Сечение призмы плоскостью рассмотрим на примере сечения пятигранной призмы ABCDE, ребра которой перпендикулярны горизонтальной плоскости проекции, а секущая плоскость α общего положения задана следами.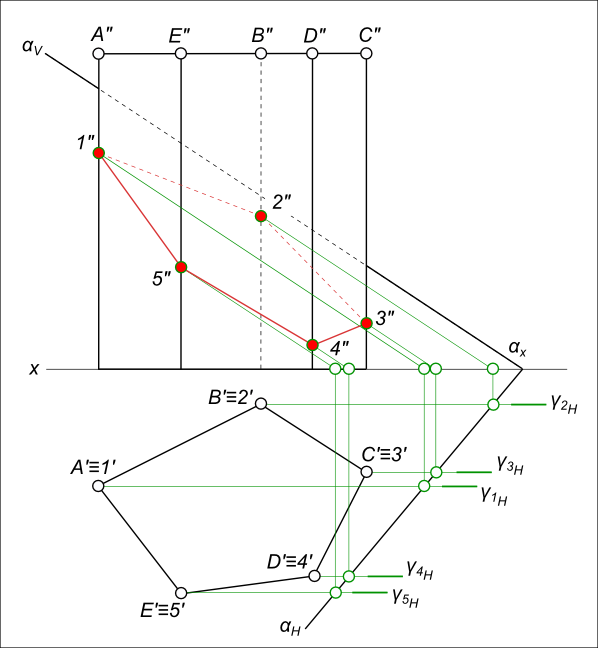

Сечение призмы плоскостью

Ребра призмы - проецирующие прямые к плоскости проекций H. В данном случае, чтобы найти сечение призмы плоскостью необходимо найти точки встречи каждой проецирующей прямой с плоскостью α.
Через ребра призмы проводим плоскости уровня параллельные фронтальной плоскости проекций: γ₁, γ₂, γ₃, γ₄, γ₅. Линии пересечения данных плоскостей с секущей плоскостью α - фронтальные прямые. Пересечение фронтальных прямых с ребрами призмы определит точки пересечения последних с плоскостью α: 1", 2", 3", 4" и 5". Соединив, которые прямыми линиями, получим искомое сечение призмы плоскостью.

Определить сечение призмы плоскостью общего положения α, заданной параллельными прямыми a и b.

Сечение призмы плоскостью

Решаем эту задачу путем нахождения точек встречи ребер призмы с плоскостью α. Для этого:
- заключаем ребра призмы в горизонтально-проецирующие плоскости γ₁, γ₂, γ₃ и γ₄;
- находим линии пересечения этих плоскостей с плоскостью α (прямые 1, 2; 3, 4; 5, 6; 7, 8);
- отмечаем точки пересечения этих прямых с соответствующими ребрами призмы K", L", M" и N" ⇒ K`, L`, M` и N";
- найденные точки соединяем прямыми линиями и получаем искомое сечение призмы плоскостью α.