Развертка поверхностей

Чтобы развертка поверхностей осуществлялась, их необходимо представлять как гибкую, нерастяжимую пленку. Представленные таким образом поверхности можно путем распрямления совместить с плоскостью. Если отсек поверхности может быть совмещен с плоскостью без разрывов, то такую поверхность называют развертывающейся, а полученнуюплоскую фигуру - ее разветкой.

Поверхности, которые не могут быть совмещены с плоскостью из-за разрывов, относятся к неразвертываемым поверхностям. К группе для которой возможна развертка поверхностей могут быть отнесены только линейчатые поверхности и, в частности, те из них, которые имеют пересекющиеся смежные образующие. Точка пересечения может быть собственной - поверхности с ребром возврата и конические, и несобственной - поверхности цилиндрические.

Рассмотрим развертывание конической поверхности α на плоскость β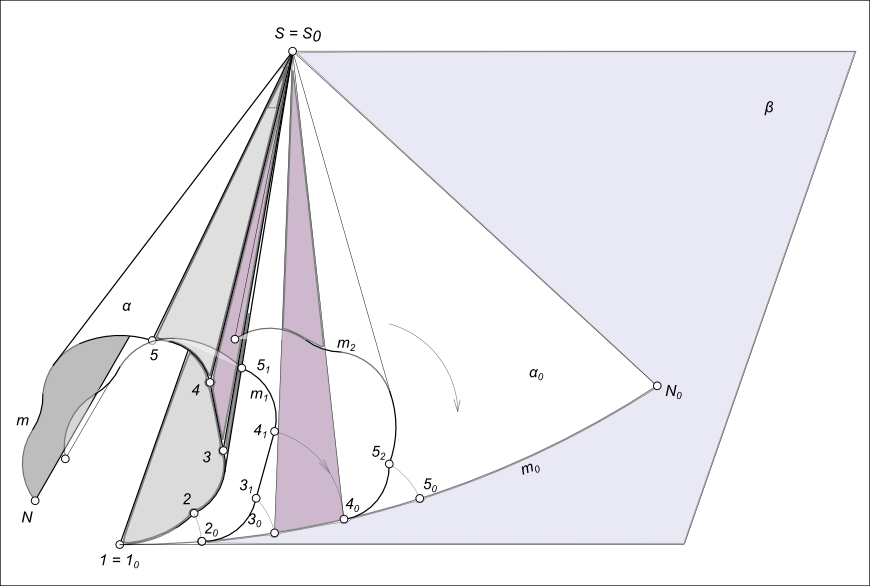

Развертка поверхностей

Развертка поверхностей сопровождается постепенным спрямлением поверхности α и ее совмещением с плоскостью β, касательной к ней. Линия касания - образующая 1S. Проведем из точки 2, на направляющей конической поверхности m, образующую конической поверхности 2S. Если расстояние между точками 1 и 2 мало, то Δ1S2 можно с определенной степенью точности отождествлять с отсеком конической поверхности, заключенной между образующими 1S и 2S. Поворачивая Δ1S2 вокруг стороны 1S до его совмещения с плоскостью β, получим Δ1S2₀, представляющий развертку отсека поверхности α 1S2 на плоскость β. При перемещении точки 2 в положение 2₀ направляющая конической поверхности m займет положение m₁. Проведя такие же действия к точкам 3; 4; ...; N получим развертку поверхности α на плоскость β.

Развертка поверхностей представлена в следующих статьях:
Графическая работа 7 - призма и пирамида;
Графическая работа 8 - развертки поверхностей вращения цилиндра и конуса
Графическая работа 12 - развертки поверхности усеченной пирамиды.
Графическая работа 13 - развертки поверхности усеченного прямого кругового конуса.
Графическая работа 14 - развертки боковой поверхности конуса.