Развертка конуса

Развертка конуса строится таким же способом, который используются при развертывании боковой поверхности пирамиды - способом треугольников. Коническая поверхность заменяется многогранной пирамидальной поверхностью, вписанной в данную коническую.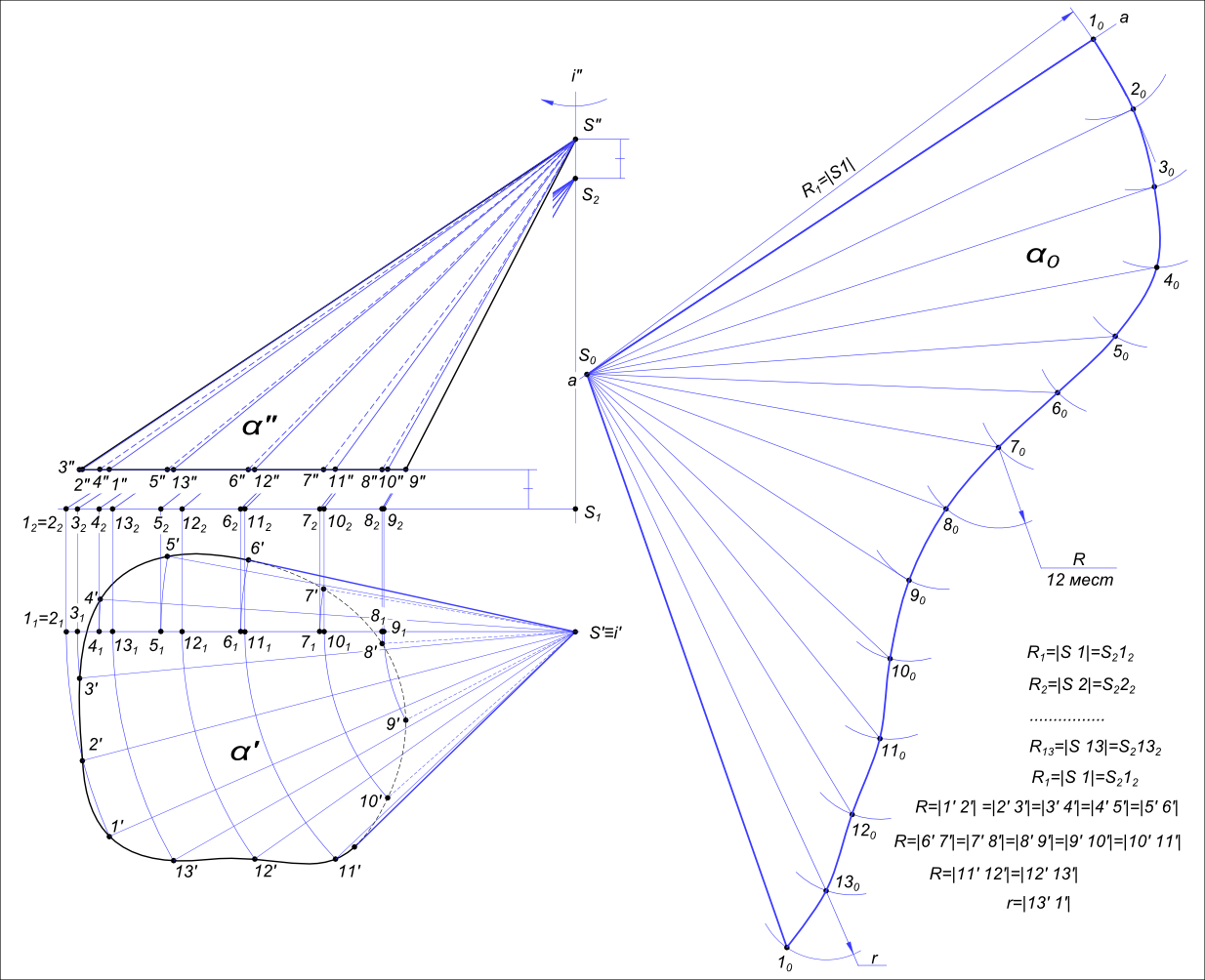

Развертка конуса

                         Развертка конуса вращения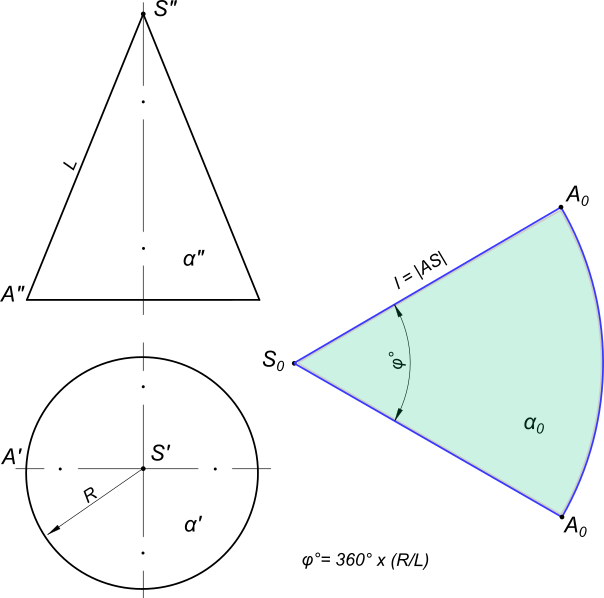

Развертка конуса

                         представляет круговой сектор, радиус которого равен длине образующей конической поверхности L = |SA|, а центральный угол: φ = 360° *(R/L).

Развертка конуса вращения усеченного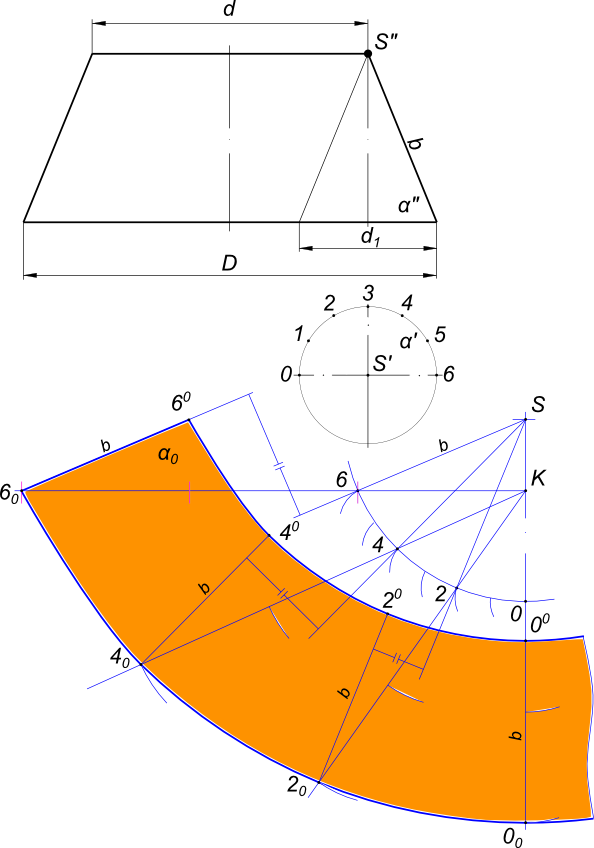

Развертка конуса

На рисунке представлено построение развертки боковой поверхности усеченного конуса без построения его вершины:
- на чертеже усеченного конуса строится вспомогательный конус подобный заданному из условия K=D/d₁, K - коэффициент кратности оснований конусов целое число. Принимаем K=3;
- разделим половину окружности основания d₁ на 6 равных частей;
- строим развертку вспомогательного конуса с вершиной S по точкам на дуге развертки;
- на оси симметрии развертки (биссектриса полной развертки) выбрать произвольную точку K и провести семейство лучей , соединяющих ее с точками 0, 2, 4, 6 развертки вспомогательного конуса;
- откладываем на проведенных лучах отрезки, величины которых равны: KO₀ = K*K0; K2₀ = K*K2; K4₀ = K*K4; K6₀ = K*K6;
- через построенные точки 0₀, 2₀, 4₀, 6₀ проводим прямые параллельные соответствующим образующим развертки вспомогательного конуса, откладывая на них натуральную величину b образующей усеченного конуса и отмечая при этом точки O⁰, 2⁰, 4⁰, 6⁰;
- соединяем построенные точки плавными линиями и получаем искомую развертку.

Развертка конуса вращения усеченного плоскостью общего положения выполнено в Графическая работа 13.