Способ нормального сечения

Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

Способ нормального сечения применяется для развертки призматических гранных поверхностей. Отличительная особенность данного способа является построение сечения призмы плоскостью нормальной (перпендикулярной) по отношению к ее боковым ребрам. При последующем развертывании призмы линия нормального сечения выстраивается в прямую линию и используется для откладывания от нее натуральной величины отрезков боковых ребер.

Построить развертку наклонной трехгранной призмы ABCDEF, иcпользуя способ нормального сечения.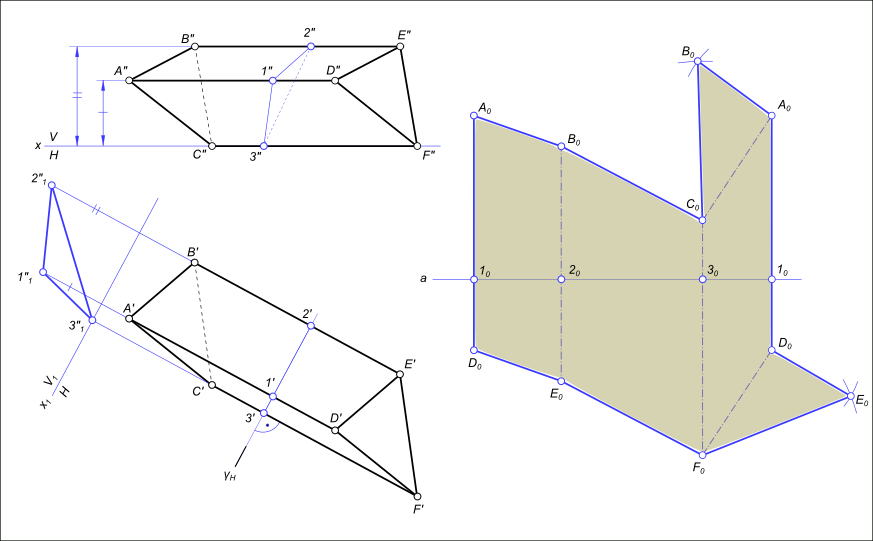

Способ нормального сечения

Построим сечение заданной призмы вспомогательной плоскостью γ_H перпендикулярной к ее боковым ребрам и горизонтальной плоскости проекций H. Методом перемены плоскостей проекций определяем действительную величину сторон Δ123. В произвольном месте эпюра проводим горизонтально прямую a. От точки 1₀, отмеченной на этой прямой, откладываем отрезки [1₀2₀], [2₀3₀], [3₀1₀], конгруентные сторонам Δ123. Через точки 1₀2₀3₀ и 1₀ проводим прямые перпендикулярные к прямой a, и откладываем на них от точек 1₀2₀3₀ и 1₀ отрезки, конгруентные соответствующим действительным величинам отрезков боковых ребер. Полученные точки A₀B₀C₀A и D₀E₀ F₀D₀ соединяем прямыми. Ребра AD, BE, и CF параллельны плоскости H, поэтому на нее они проецируются в действительную величину. Плоская фигура A₀B₀C₀A₀D₀E₀F₀D₀ - развертка боковой поверхности призмы. К ней пристроены основания призмы ΔA₀B₀C₀ и ΔD₀E₀F₀.

Способ нормального сечения применяется также для получения развертки цилиндрической поверхности: Развертка цилиндра