Способ треугольников

Разверткой многогранника называется плоская фигура, получаемая последовательным совмещением всех граней многогранника с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

Способ треугольников используют для построения развертки поверхности пирамиды. Развертка боковой поверхности пирамиды - плоская фигура, состоящая из треугольников - граней пирамиды. Поэтому построение развертки поверхности пирамиды сводится к определению действительной величины ребер пирамиды и построению по трем известным сторонам треугольников - граней пирамиды.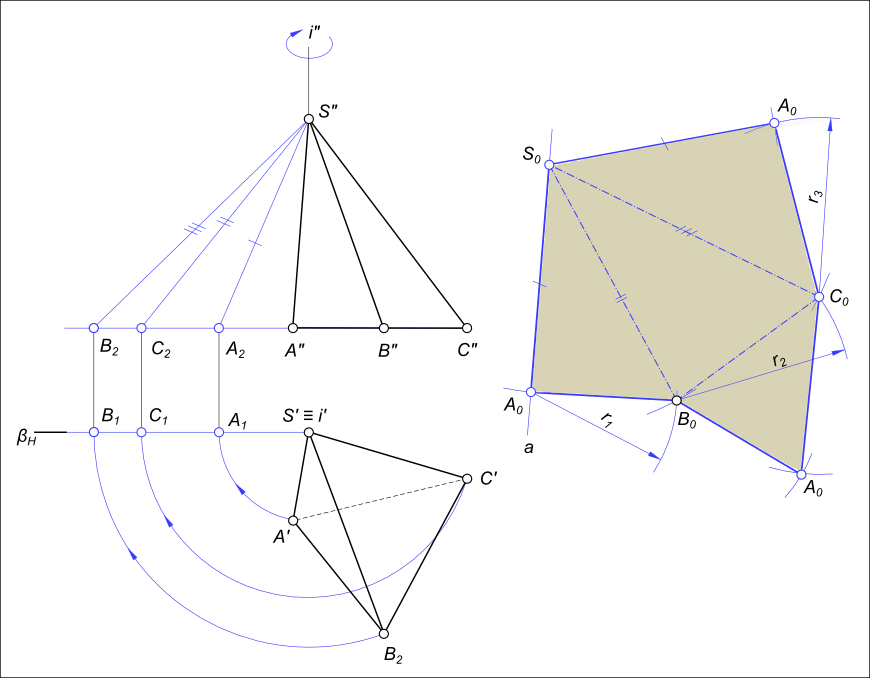

Способ треугольников

Вращаем ребра вокруг оси i (i⊥H и i∋S) и совмещаем с плоскостью β (плоскость β║V β∋i). Выполняем определение действительных величин ребер пирамиды [S"A₂], [S"B₂], [S"C₂]. Приступая к построению развертки проводим произвольную прямую a через произвольную точку S₀. Откладываем на ней от точки S₀ отрезок [S₀A₀]≅ [S"A₂]. Из точки A₀ проводим дугу радиусом r₁=‌A`B`‌, а из точки S₀ - дугу радиусом R₁=‌S"B₂. Пересечение дуг укажет положение вершины B₀ ΔS₀A₀B₀ (ΔS₀A₀B₀≅ΔSAB - грани пирамиды). Аналогично определяем положение точек C₀ и A₀. Соединяя точки A₀B₀C₀A₀S₀, получим развертку боковой поверхности. Присоединив к какой-либо стороне (ребру) основание (ΔABC) - получаем полную развертку поверхности пирамиды SABC.

Способ треугольников использован для построения развертки поверхности усеченной пирамиды в графической работе №12: Графическая работа 12