Свойства развертки поверхностей

С позиции теории множеств поверхность и ее развертку следует рассматривать как два точечных множества. Так как, по определению, развертка поверхности представляет собой плоскую фигуру, образованную из поверхности без разрывов, то между данными двумя множествами устанавливается взаимно-однозначное соответствие: каждой точке (фигуре) на поверхности соответствует точка (фигура) на развертке и наоборот. Фигура 1S2, образованная подмножеством точек, принадлежащих поверхности α, конгруентна фигуре 1S2₀, принадлежащей развертке α₀. Аналогично (Δ2S3 ⊂ α) ≅ (2₀S3₀) и т. д.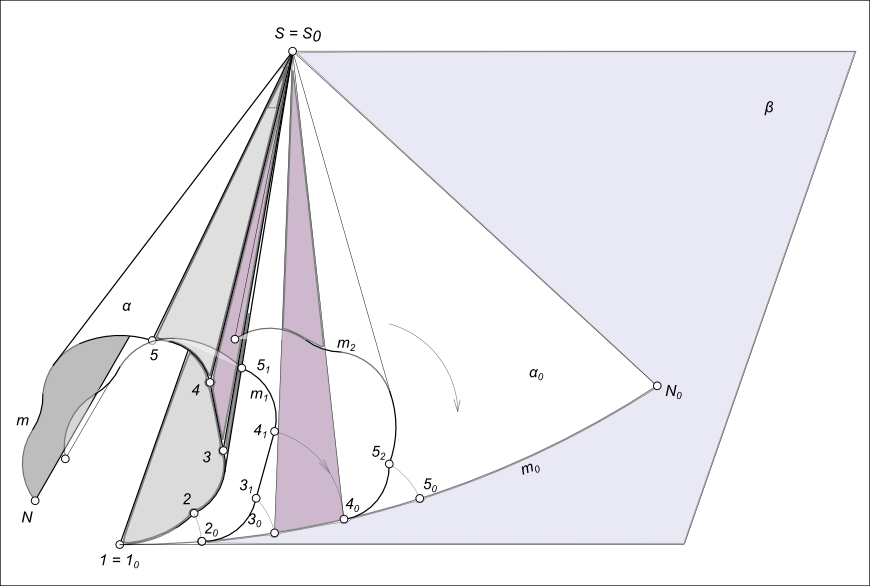

Свойства развертки поверхностей

Отсюда следует, что расстояние между точками 1 и 2 или любыми другими точками, взятыми на фигуре 1S2, равно расстоянию между точками 1₀ и 2₀ фигуры 1₀S2₀. На основании этого сформулирован ряд свойств: - Длины двух соответствующих линий поверхности и ее развертки равны между собой. Следствием этого является - замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают одинаковую площадь; - Угол между линиями на поверхности равен углу между соответствующими линиями на развертке; - Прямой на поверхности соответствует такая же прямая на развертке (обратное утверждение не имеет смысла); - Параллельным прямым на поверхности соответствует также параллельные прямые на развертке; - Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.