Эпюра плоскости

Задача № 1. Эпюра плоскости α задана следами αH и αV. Треугольник ∆ABC, лежащий в плоскости α, задан проекцией ∆A`B`C`. Построить недостающую проекцию треугольника ∆A"B"C", используя главные линии плоскости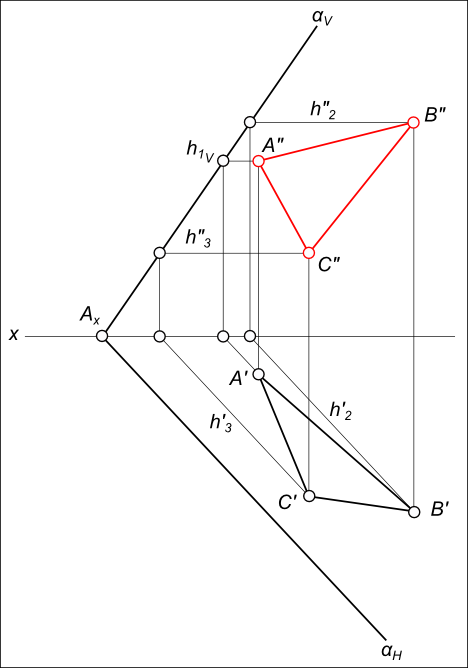

Эпюра плоскости

Задача № 2. На построение эпюра плоскости равностороннего треугольника ABC,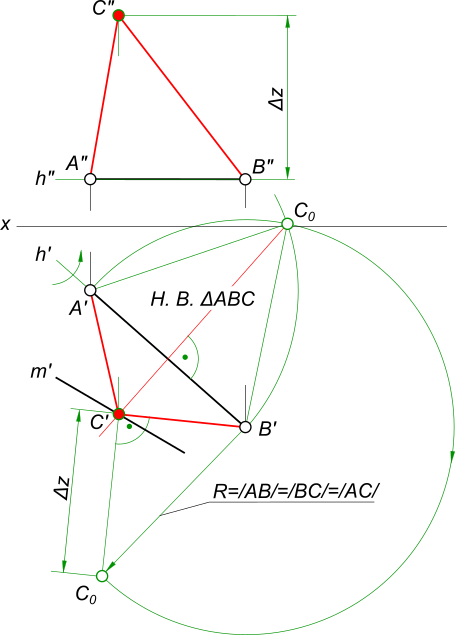

Эпюра плоскости

с основанием AB(A`B`, ...), которое принадлежит горизонтальной прямой h(h`, h"), а вершина C принадлежит прямой m`. Построить недостающие проекции треугольника.
Эпюра плоскости равностороннего треугольника ABC, строится по следующему плану:
- отрезок AB - одна из сторон треугольника, представляет собой прямую уровня - горизонтальную прямую так как A"B" || Ox. На горизонтальную плоскость проекции он проецируется в натуральную величину.
Выполняем построение BC:
- строим натуральную величину равностороннего треугольника ABC, которая может быть получена вращением вокруг горизонтали h;
- в пересечении плоскости траектории движения точки C с прямой m` получим C`.
По способу прямоугольного треугольника определяем Δz = zC-zB:
- из центра O≡B` описываем дугу радиусом R=|AB|=|BC|=|CA| до пересечения с направлением перпендикуляра в точке C0;
- определяем разницу аппликат катета BC - Δz.
Откладываем Δz на фронтальной плоскости проекций от точки B" и по линии проекционной связи находим точку C".

Задача № 3. Эпюра плоскости α задана следами αH и αV. Треугольник ∆ABC, лежащий в плоскости α, задан проекцией ∆A"B"C". Построить недостающую проекцию треугольника ∆A`B`C`, используя прямые общего положения в плоскости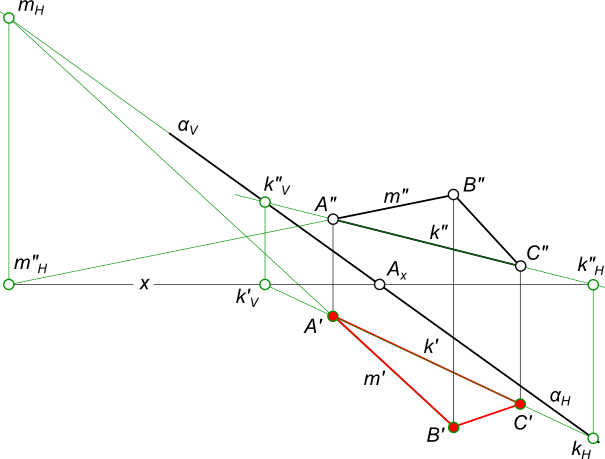

Эпюра плоскости

Эпюра плоскости треугольника ABC, строится по следующему плану:
- выбираем стороны треугольника соответствующие определению прямых общего положения. Это отрезок AB прямой m и отрезок AC прямой k;
- находим их горизонтальные проекции, построив следы прямых m и k;
- находим горизонтальные проекции вершин треугольника по линиям проекционной связи, как принадлежащие прямым m и k.